Advertisements
Advertisements
प्रश्न
The formula `(vec"a" + vec"b")^2 = vec"a"^2 + vec"b"^2 + 2vec"a" xx vec"b"` is valid for non-zero vectors `vec"a"` and `vec"b"`
पर्याय
True
False
उत्तर
This statement is False.
Explanation:
`(vec"a" + vec"b")^2 = (vec"a" + vec"b") * (vec"a" + vec"b")`
= `|vec"a"|^2 + |vec"b"|^2 + 2vec"a" * vec"b"`
APPEARS IN
संबंधित प्रश्न
Write a unit vector making equal acute angles with the coordinates axes.
Write the position vector of a point dividing the line segment joining points A and B with position vectors \[\vec{a}\] and \[\vec{b}\] externally in the ratio 1 : 4, where \[\overrightarrow{a} = 2 \hat{i} + 3 \hat{j} + 4 \hat{k} \text{ and }\overrightarrow{b} = - \hat{i} + \hat{j} + \hat{k} .\]
For what value of 'a' the vectors \[2 \hat{i} - 3 \hat{j} + 4 \hat{k} \text{ and }a \hat{i} + 6 \hat{j} - 8 \hat{k}\] are collinear?
Forces 3 O \[\vec{A}\], 5 O \[\vec{B}\] act along OA and OB. If their resultant passes through C on AB, then
Let G be the centroid of ∆ ABC. If \[\overrightarrow{AB} = \vec{a,} \overrightarrow{AC} = \vec{b,}\] then the bisector \[\overrightarrow{AG} ,\] in terms of \[\vec{a}\text{ and }\vec{b}\] is
Find the vector equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0. Hence find whether the plane thus obtained contains the line \[\frac{x + 2}{5} = \frac{y - 3}{4} = \frac{z}{5}\] or not.
Find the components along the coordinate axes of the position vector of the following point :
P(3, 2)
The vector `bar"a"` is directed due north and `|bar"a"|` = 24. The vector `bar"b"` is directed due west and `|bar"b"| = 7`. Find `|bar"a" + bar"b"|`.
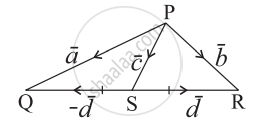
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Select the correct option from the given alternatives:
The volume of tetrahedron whose vectices are (1,-6,10), (-1, -3, 7), (5, -1, λ) and (7, -4, 7) is 11 cu units, then the value of λ is
Select the correct option from the given alternatives:
Let a, b, c be distinct non-negative numbers. If the vectors `"a"hat"i" + "a"hat"j" + "c"hat"k" , hat"i" + hat"k" "and" "c"hat"i" + "c"hat"j" + "b"hat"k"` lie in a plane, then c is
In a parallelogram ABCD, diagonal vectors are `bar"AC" = 2hat"i" + 3hat"j" + 4hat"k" and bar"BD" = - 6hat"i" + 7hat"j" - 2hat"k"`, then find the adjacent side vectors `bar"AB" and bar"AD"`.
If `bar"OA" = bar"a" and bar"OB" = bar"b",` then show that the vector along the angle bisector of ∠AOB is given by `bar"d" = lambda(bar"a"/|bar"a"| + bar"b"/|bar"b"|).`
Dot product of a vector with vectors `3hat"i" - 5hat"k", 2hat"i" + 7hat"j" and hat"i" + hat"j" + hat"k"` are respectively -1, 6 and 5. Find the vector.
Show that no line in space can make angles `pi/6` and `pi/4` with X-axis and Y-axis.
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a".(bar"b".bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`(bar"a" xx bar"b").(bar"c"xxbar"d")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`|bar"a"|. (bar"b" + bar"c")`
Find the volume of the parallelopiped spanned by the diagonals of the three faces of a cube of side a that meet at one vertex of the cube.
If the points (–1, –1, 2), (2, m, 5) and (3,11, 6) are collinear, find the value of m.
Using vectors, prove that cos (A – B) = cosA cosB + sinA sinB.
`bara, barb` and `barc` are three vectors such that `veca + vecb + vecc` 20, `|bara| = 1, |barb| = 2` and `|barc| = 3`. Then `bara. barb + barb.barc + bar(c.a)` is equal to
Let `bara, barb` and `barc` be three vectors, then `bara xx (barb xx barc) = (bara xx barb) xx barc` if
If two or more vectors are parallel to the same line, such vectors are known as:
Let the vectors `vec(a)` such `vec(b)` that `|veca|` = 3 and `|vecb| = sqrt(2)/3`, then `veca xx vecb` is a unit vector if the angle between `veca` and `vecb` is
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
Check whether the vectors `2 hati+2 hatj+3 hatk,-3 hati+3 hatj+2 hatk and 3 hati +4 hatk` form a triangle or not.
In the triangle PQR, `bar(PQ) = 2bara and bar(QR) = 2barb`. The mid-point of PR is M. Find the following vectors in terms of `bara and barb`.
- `bar(PR)`
- `bar(PM)`
- `bar(QM)`
Check whether the vectors `2hati + 2hatj +3hatk, - 3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
