Advertisements
Advertisements
प्रश्न
Forces 3 O \[\vec{A}\], 5 O \[\vec{B}\] act along OA and OB. If their resultant passes through C on AB, then
पर्याय
C is a mid-point of AB
C divides AB in the ratio 2 : 1
3 AC = 5 CB
2 AC = 3 CB
उत्तर
3 AC = 5 CB
Draw ON, the perpendicular to the line AB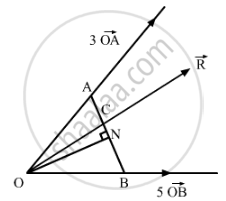
Let
\[\vec{i}\] be the unit vector along ON
The resultant force \[\vec{R} = 3 \overrightarrow{OA} + 5 \overrightarrow{OB} . . . . . \left( 1 \right)\]
The angles between \[\vec{i}\] and the forces \[\vec{R} , 3 \overrightarrow{OA} , 5 \overrightarrow{OB}\] are ∠CON, ∠AON, ∠BON respectively.
\[\vec{R} \cdot \vec{i} = 3 \overrightarrow{OA} \cdot \vec{i} + 5 \overrightarrow{OB} \cdot \vec{i}\]
⇒ R⋅1⋅ cos ∠CON = 3
\[\overrightarrow{OA}\]⋅1⋅cos∠AON + 5
\[\overrightarrow{OB}\]⋅1⋅cos∠BON
\[R \cdot \frac{ON}{OC} = 3OA \times \frac{ON}{OA} + 5OB\frac{ON}{OB}\]
\[\frac{R}{OC} = \left( 3 + 5 \right)\]
R = 8
\[\overrightarrow{OC}\]
We know that,
\[\overrightarrow{OA} = \overrightarrow{OC} + \overrightarrow{CA} \]
\[ \Rightarrow 3 \overrightarrow{OA} = 3 \overrightarrow{OC} + 3 \overrightarrow{CA} . . . . . \left( i \right)\]
\[ \overrightarrow{OB} = \overrightarrow{OC} + \overrightarrow{CB} \]
\[ \Rightarrow 5 \overrightarrow{OB} = 5 \overrightarrow{OC} + 5 \overrightarrow{CB} . . . . . \left( ii \right)\]
on adding (i) and (ii) we get,
\[3 \overrightarrow{OA} + 5 \overrightarrow{OB} = 8 \overrightarrow{OC} + 3 \overrightarrow{CA} + 5 \overrightarrow{CB} \]
\[\vec{R} = 8 \overrightarrow{OC} + 3 \overrightarrow{CA} + 5 \overrightarrow{CB} \]
\[8 \overrightarrow{OC} = 8 \overrightarrow{OC} + 3 \overrightarrow{CA} + 5 \overrightarrow{CB}\]
\[\left| 3 \overrightarrow{AC} \right| = \left| 5 \overrightarrow{CB} \right|\]
\[ \Rightarrow 3AC = 5CB\]
APPEARS IN
संबंधित प्रश्न
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] represent the sides of a triangle taken in order, then write the value of \[\vec{a} + \vec{b} + \vec{c} .\]
If D, E, F are the mid-points of the sides BC, CA and AB respectively of a triangle ABC, write the value of \[\overrightarrow{AD} + \overrightarrow{BE} + \overrightarrow{CF} .\]
If a vector makes angles α, β, γ with OX, OY and OZ respectively, then write the value of sin2 α + sin2 β + sin2 γ.
If \[\overrightarrow{a} = \hat{i} + \hat{j} , \vec{b} = \hat{j} + \hat{k} \text{ and }\vec{c} = \hat{k} + \hat{i} ,\] write unit vectors parallel to \[\overrightarrow{a} + \overrightarrow{b} - 2 \overrightarrow{c} .\]
Find a unit vector in the direction of \[\overrightarrow{a} = 2 \hat{i} - 3 \hat{j} + 6 \hat{k}\].
Write a unit vector in the direction of \[\overrightarrow{PQ}\], where P and Q are the points (1, 3, 0) and (4, 5, 6) respectively.
In a triangle OAC, if B is the mid-point of side AC and \[\overrightarrow{OA} = \overrightarrow{a} , \overrightarrow{OB} = \overrightarrow{b}\], then what is \[\overrightarrow{OC}\].
The vector equation of the plane passing through \[\vec{a} , \vec{b} , \vec{c} ,\text{ is }\vec{r} = \alpha \vec{a} + \beta \vec{b} + \gamma \vec{c} ,\] provided that
If ABCDEF is a regular hexagon, then \[\overrightarrow{AD} + \overrightarrow{EB} + \overrightarrow{FC}\] equals
Find the vector equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0. Hence find whether the plane thus obtained contains the line \[\frac{x + 2}{5} = \frac{y - 3}{4} = \frac{z}{5}\] or not.
Find the components along the coordinate axes of the position vector of the following point :
S(4, –3)
If` vec"a" = 2hat"i" + 3hat"j" + + hat"k", vec"b" = hat"i" - 2hat"j" + hat"k" "and" vec"c" = -3hat"i" + hat"j" + 2hat"k", "find" [vec"a" vec"b" vec"c"]`
Select the correct option from the given alternatives:
The volume of tetrahedron whose vectices are (1,-6,10), (-1, -3, 7), (5, -1, λ) and (7, -4, 7) is 11 cu units, then the value of λ is
If P is orthocentre, Q is the circumcentre and G is the centroid of a triangle ABC, then prove that `bar"QP" = 3bar"QG"`.
Express the vector `bar"a" = 5hat"i" - 2hat"j" + 5hat"k"` as a sum of two vectors such that one is parallel to the vector `bar"b" = 3hat"i" + hat"k"` and other is perpendicular to `bar"b"`.
Find a unit vector perpendicular to the plane containing the point (a, 0, 0), (0, b, 0) and (0, 0, c). What is the area of the triangle with these vertices?
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a" xx (bar"b".bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a" xx(bar"b" xx bar"c")`
The points A(- a, -b), B (0, 0), C(a, b) and D(a2 , ab) are ______.
Find a vector of magnitude 11 in the direction opposite to that of `vec"PQ"` where P and Q are the points (1, 3, 2) and (–1, 0, 8), respectively.
Find a unit vector in the direction of `vec"PQ"`, where P and Q have co-ordinates (5, 0, 8) and (3, 3, 2), respectively
If `vec"a", vec"b", vec"c"` determine the vertices of a triangle, show that `1/2[vec"b" xx vec"c" + vec"c" xx vec"a" + vec"a" xx vec"b"]` gives the vector area of the triangle. Hence deduce the condition that the three points `vec"a", vec"b", vec"c"` are collinear. Also find the unit vector normal to the plane of the triangle.
If `vec"a", vec"b", vec"c"` are unit vectors such that `vec"a" + vec"b" + vec"c"` = 0, then the value of `vec"a" * vec"b" + vec"b" * vec"c" + vec"c" * vec"a"` is ______.
If `vec"r" * vec"a" = 0, vec"r" * vec"b" = 0` and `vec"r" * vec"c" = 0` for some non-zero vector `vec"r"`, then the value of `vec"a" * (vec"b" xx vec"c")` is ______.
The values of k for which `|"k"vec"a"| < |vec"a"|` and `"k"vec"a" + 1/2 vec"a"` is parallel to `vec"a"` holds true are ______.
Let `veca, vecb` and `vecc` be three unit vectors such that `veca xx (vecb xx vecc) = sqrt(3)/2 (vecb + vecc)`. If `vecb` is not parallel to `vecc`, then the angle between `veca` and `vecc` is
For given vectors, `veca = 2hati - hatj + 2hatk` and `vecb = - hati + hatj - hatk` find the unit vector in the direction of the vector `veca + vecb`.
Find `|vecx|` if `(vecx - veca).(vecx + veca)` = 12, where `veca` is a unit vector.
The angles of a triangle, two of whose sides are represented by the vectors `sqrt(3)(veca xx vecb)` and `vecb - (veca.vecb)veca` where `vecb` is a non-zero vector and `veca` is a unit vector are ______.
Check whether the vectors `2hati + 2hatj + 3hat k, -3hati + 3hatj + 2hat k` and `3hati + 4hatk` form a triangle or not.
Check whether the vectors`2hati+2hatj+3hatk,-3hati+3hatj+2hatk and 3hati +4hatk` form a triangle or not.
In the triangle PQR, `bar(PQ)` = `2bara` and `bar(QR)` = `2barb`. The mid-point of PR is M. Find following vectors in terms of `bara` and `barb`.
(i) `bar(PR)` (ii) `bar(PM)` (iii) `bar(QM)`
If `|veca| = 3, |vecb| = sqrt(2)/3` and `veca xx vecb` is a unit vector then the angle between `veca` and `vecb` will be ______.
In the triangle PQR, `bar(PQ)=2bara` and `bar(QR)=2barb`. The mid-point of PR is M. Find following vectors in terms of `bara and barb`.
(i) `bar(PR)` (ii) `bar(PM)` (iii) `bar(QM)`
In the triangle PQR, `bar"PQ" = 2 bar" a" and bar"QR" = 2 bar"b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`
Check whether the vectors `2 hati+2 hatj+3 hatk,-3 hati+3 hatj+2 hatk and 3 hati +4 hatk` form a triangle or not.
