Question

Forces 3 O \[\vec{A}\], 5 O \[\vec{B}\] act along OA and OB. If their resultant passes through C on AB, then 

Options

• C is a mid-point of AB

• C divides AB in the ratio 2 : 1

• 3 AC = 5 CB

• 2 AC = 3 CB

Answer 1

3 AC = 5 CB
Draw ON, the perpendicular to the line AB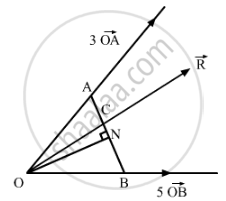

Let
\[\vec{i}\]  be the unit vector along ON
The resultant force \[\vec{R} = 3 \overrightarrow{OA} + 5 \overrightarrow{OB} . . . . . \left( 1 \right)\]
The angles between \[\vec{i}\]  and the forces \[\vec{R} , 3 \overrightarrow{OA} , 5 \overrightarrow{OB}\] are ∠CON, ∠AON, ∠BON respectively.
\[\vec{R} \cdot \vec{i} = 3 \overrightarrow{OA} \cdot \vec{i} + 5 \overrightarrow{OB} \cdot \vec{i}\]
⇒ R⋅1⋅ cos ∠CON = 3
\[\overrightarrow{OA}\]⋅1⋅cos∠AON + 5
\[\overrightarrow{OB}\]⋅1⋅cos∠BON
\[R \cdot \frac{ON}{OC} = 3OA \times \frac{ON}{OA} + 5OB\frac{ON}{OB}\]
\[\frac{R}{OC} = \left( 3 + 5 \right)\]
R = 8
\[\overrightarrow{OC}\]
We know that,
\[\overrightarrow{OA} = \overrightarrow{OC} + \overrightarrow{CA} \]
\[ \Rightarrow 3 \overrightarrow{OA} = 3 \overrightarrow{OC} + 3 \overrightarrow{CA} . . . . . \left( i \right)\]
\[ \overrightarrow{OB} = \overrightarrow{OC} + \overrightarrow{CB} \]
\[ \Rightarrow 5 \overrightarrow{OB} = 5 \overrightarrow{OC} + 5 \overrightarrow{CB} . . . . . \left( ii \right)\]
on adding (i) and (ii) we get,
\[3 \overrightarrow{OA} +  5 \overrightarrow{OB} = 8 \overrightarrow{OC}  +  3 \overrightarrow{CA}  +  5 \overrightarrow{CB} \]
\[\vec{R}  =  8 \overrightarrow{OC}  +  3 \overrightarrow{CA}  +  5 \overrightarrow{CB} \]
\[8 \overrightarrow{OC}  =  8 \overrightarrow{OC}  +  3 \overrightarrow{CA}  +  5 \overrightarrow{CB}\]
\[\left| 3 \overrightarrow{AC} \right| = \left| 5 \overrightarrow{CB} \right|\]
\[ \Rightarrow 3AC = 5CB\]