Advertisements
Advertisements
Question
Find the area of the traingle with vertices (1, 1, 0), (1, 0, 1) and (0, 1, 1).
Solution
Let A = (1, 1, 0), B = (1, 0, 1), C = (0, 1, 1)
|AB| = `sqrt((1 - 1)^2 + (1 - 0)^2 + (0 - 1)^2) = sqrt(0 + 1 + 1) = sqrt2`
|BC| = `sqrt((1 - 0)^2 + (0 - 1)^2 + (1 - 1)^2) = sqrt(1 + 1 + 0) = sqrt2`
|CA| = `sqrt((0 - 1)^2 + (1 - 1)^2 + (1 - 0)^2) = sqrt(1 + 0 + 1) = sqrt2`
∴ |AB| = |BC| = |CA|
∴ Triangle is an equilateral triangle
∴ Its area = `sqrt3/4 ("side")^2`
`= sqrt3/4 (sqrt2)^2`
`= sqrt3/2` sq.units.
APPEARS IN
RELATED QUESTIONS
If \[\overrightarrow{a}\], \[\overrightarrow{b}\], \[\overrightarrow{c}\] are the position vectors of the vertices of a triangle, then write the position vector of its centroid.
Write the position vector of a point dividing the line segment joining points A and B with position vectors \[\vec{a}\] and \[\vec{b}\] externally in the ratio 1 : 4, where \[\overrightarrow{a} = 2 \hat{i} + 3 \hat{j} + 4 \hat{k} \text{ and }\overrightarrow{b} = - \hat{i} + \hat{j} + \hat{k} .\]
Write a unit vector in the direction of \[\overrightarrow{a} = 3 \hat{i} + 2 \hat{j} + 6 \hat{k} .\]
Find the value of 'p' for which the vectors \[3 \hat{i} + 2 \hat{j} + 9 \hat{k}\] and \[\hat{i} - 2p \hat{j} + 3 \hat{k}\] are parallel.
Write the position vector of the point which divides the join of points with position vectors \[3 \overrightarrow{a} - 2 \overrightarrow{b}\text{ and }2 \overrightarrow{a} + 3 \overrightarrow{b}\] in the ratio 2 : 1.
If \[\vec{a}\text{ and }\vec{b}\] are two collinear vectors, then which of the following are incorrect?
Find the components along the coordinate axes of the position vector of the following point :
R(–11, –9)
Find the position vector of the mid-point of the vector joining the points
In Figure, which of the following is not true?
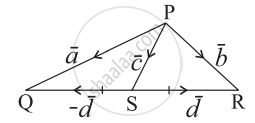
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Select the correct option from the given alternatives:
If l, m, n are direction cosines of a line then `"l"hat
"i" + "m"hat"j" + "n"hat"k"` is ______
If two sides of a triangle are `hat"i" + 2hat"j" and hat"i" + hat"k"`, find the length of the third side.
Two sides of a parallelogram are `3hat"i" + 4hat"j" - 5hat"k"` and `-2hat"j" + 7hat"k"`. Find the unit vectors parallel to the diagonals.
Find the unit vectors that are parallel to the tangent line to the parabola y = x2 at the point (2, 4).
If `bar"a", bar"b", bar"c"` are unit vectors such that `bar"a" + bar"b" + bar"c" = bar0,` then find the value of `bar"a".bar"b" + bar"b".bar"c" + bar"c".bar"a".`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a".(bar"b".bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`(bar"a".bar"b") xx (bar"c".bar"d")`
The XZ plane divides the line segment joining the points (3, 2, b) and (a, -4, 3) in the ratio ______.
If `overline"u"` and `overline"v"` are unit vectors and θ is the acute angle between them, then `2overline"u" xx 3overline"v"` is a unit vector for ______
Using vectors, prove that cos (A – B) = cosA cosB + sinA sinB.
The 2 vectors `hat"j" + hat"k"` and `3hat"i" - hat"j" + 4hat"k"` represents the two sides AB and AC, respectively of a ∆ABC. The length of the median through A is ______.
Find a unit vector in the direction of `vec"PQ"`, where P and Q have co-ordinates (5, 0, 8) and (3, 3, 2), respectively
The vector `vec"a" + vec"b"` bisects the angle between the non-collinear vectors `vec"a"` and `vec"b"` if ______.
Classify the following measures as scalar and vector.
40°
Classify the following as scalar and vector quantity.
Distance
The unit vector perpendicular to the vectors `6hati + 2hatj + 3hatk` and `3hati - 6hatj - 2hatk` is
Four vectors `veca, vecb, vecc` and `vecx` satisfy the relation `(veca.vecx)vecb = vecc + vecx` where `vecb * veca` ≠ 1. The value of `vecx` in terms of `veca, vecb` and `vecc` is equal to
If `veca` and `vecb` are two collinear vectors then which of the following are incorrect.
In the triangle PQR, `bar("P""Q")`= `2 bar"a"` and `bar ("QR")` = `2 barb`.The mid - point of PR is M. Find following vector in term of `bar a ` and `barb.`
- `bar("P""R")`
- `bar("P""M")`
- `bar("Q""M")`
Check whether the vectors `2hati + 2hatj + 3hatk, - 3hati + 3hatj +2 hatk and 3hati + 4hatk` from a triangle or not.
Check whether the vectors`2hati+2hatj+3hatk,-3hati+3hatj+2hatk and 3hati +4hatk` form a triangle or not.
Find the value of λ for which the points (6, – 1, 2), (8, – 7, λ) and (5, 2, 4) are collinear.
In the triangle PQR, `bar"PQ" = 2 bar" a" and bar"QR" = 2 bar"b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`
Check whether the vectors `2hati+2hatj+3hatk,-3hati+3hatj+2hatk` and `3hati+4hatk` form a triangle or not.
In the triangle PQR, `bar"PQ" = bar"2a", bar"QR" = bar"2b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`.
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
