Advertisements
Advertisements
Question
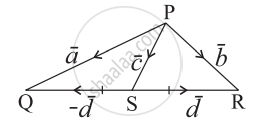
In Figure, which of the following is not true?
Options
\[\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CA} = \vec{0}\]
\[\overrightarrow{AB} + \overrightarrow{BC} - \overrightarrow{AC} = \vec{0}\]
\[\overrightarrow{AB} + \overrightarrow{BC} - \overrightarrow{CA} = \vec{0}\]
\[\overrightarrow{AB} - \overrightarrow{CB} + \overrightarrow{CA} = \vec{0}\]
Solution
\[\overrightarrow{AB} + \overrightarrow{BC} - \overrightarrow{CA} = \vec{0}\]
We have, LHS = \[\overrightarrow{AB} + \overrightarrow{BC} - \overrightarrow{CA} = \overrightarrow{AC} - \overrightarrow{CA}\] [∵ \[\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}\]
\[= - \overrightarrow{CA} - \overrightarrow{CA} \]
\[ = - 2 \overrightarrow{CA}\]
So, LHS \[\neq\] RHS
Hence, It is not true.
APPEARS IN
RELATED QUESTIONS
If `veca=xhati+2hatj-zhatk and vecb=3hati-yhatj+hatk` are two equal vectors ,then write the value of x+y+z
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] are position vectors of the vertices A, B and C respectively, of a triangle ABC, write the value of \[\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CA} .\]
Write a unit vector making equal acute angles with the coordinates axes.
If a vector makes angles α, β, γ with OX, OY and OZ respectively, then write the value of sin2 α + sin2 β + sin2 γ.
Write the position vector of a point dividing the line segment joining points A and B with position vectors \[\vec{a}\] and \[\vec{b}\] externally in the ratio 1 : 4, where \[\overrightarrow{a} = 2 \hat{i} + 3 \hat{j} + 4 \hat{k} \text{ and }\overrightarrow{b} = - \hat{i} + \hat{j} + \hat{k} .\]
If \[\overrightarrow{a} = \hat{i} + 2 \hat{j} , \vec{b} = \hat{j} + 2 \hat{k} ,\] write a unit vector along the vector \[3 \overrightarrow{a} - 2 \overrightarrow{b} .\]
Write a unit vector in the direction of \[\overrightarrow{a} = 3 \hat{i} + 2 \hat{j} + 6 \hat{k} .\]
If \[\overrightarrow{a} = \hat{i} + 2 \hat{j} - 3 \hat{k} \text{ and }\overrightarrow{b} = 2 \hat{i} + 4 \hat{j} + 9 \hat{k} ,\] find a unit vector parallel to \[\overrightarrow{a} + \overrightarrow{b}\].
Find the value of 'p' for which the vectors \[3 \hat{i} + 2 \hat{j} + 9 \hat{k}\] and \[\hat{i} - 2p \hat{j} + 3 \hat{k}\] are parallel.
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] and \[\vec{d}\] are the position vectors of points A, B, C, D such that no three of them are collinear and \[\vec{a} + \vec{c} = \vec{b} + \vec{d} ,\] then ABCD is a
Find the components along the coordinate axes of the position vector of the following point :
Q(–5, 1)
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Find a vector in the direction of `bara = hati - 2hatj` that has magnitude 7 units.
If P is orthocentre, Q is the circumcentre and G is the centroid of a triangle ABC, then prove that `bar"QP" = 3bar"QG"`.
If `bar"a", bar"b", bar"c"` are unit vectors such that `bar"a" + bar"b" + bar"c" = bar0,` then find the value of `bar"a".bar"b" + bar"b".bar"c" + bar"c".bar"a".`
Express the vector `bar"a" = 5hat"i" - 2hat"j" + 5hat"k"` as a sum of two vectors such that one is parallel to the vector `bar"b" = 3hat"i" + hat"k"` and other is perpendicular to `bar"b"`.
Find the acute angle between the curves at their points of intersection, y = x2, y = x3.
Let bar"b" = 4hat"i" + 3hat"j" and bar"c" be two vectors perpendicular to each other in the XY-plane. Find the vector in the same plane having projection 1 and 2 along bar"b" and bar"c" respectively.
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`(bar"a".bar"b") xx (bar"c".bar"d")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`(bar"a".bar"b").bar"c"`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`(bar"a".bar"b")bar"c"`
The points A(- a, -b), B (0, 0), C(a, b) and D(a2 , ab) are ______.
For 0 < θ < π, if A = `[(costheta, -sintheta), (sintheta, costheta)]`, then ______
If `vec"a" = 2hat"i" - hat"j" + hat"k", vec"b" = hat"i" + hat"j" - 2hat"k"` and `vec"c" = hat"i" + 3hat"j" - hat"k"`, find `lambda` such that `vec"a"` is perpendicular to `lambdavec"b" + vec"c"`.
If `veca` and `vecb` are unit vectors, then what is the angle between `veca` and `vecb` for `sqrt(3) veca - vecb` to be a unit vector?
The unit vector perpendicular to the vectors `hat"i" - hat"j"` and `hat"i" + hat"j"` forming a right handed system is ______.
If `vec"r" * vec"a" = 0, vec"r" * vec"b" = 0` and `vec"r" * vec"c" = 0` for some non-zero vector `vec"r"`, then the value of `vec"a" * (vec"b" xx vec"c")` is ______.
If `vec"a"` is any non-zero vector, then `(vec"a" .hat"i")hat"i" + (vec"a".hat"j")hat"j" + (vec"a".hat"k")hat"k"` equals ______.
Classify the following measures as scalar and vector.
20 m/s2
If `veca ≠ vec(0), veca.vecb = veca.vecc, veca xx vecb = veca xx vecc`, then show that `vecb = vecc`.
Let `bara, barb` and `barc` be three vectors, then `bara xx (barb xx barc) = (bara xx barb) xx barc` if
Unit vector along `vec(PQ)`, where coordinates of P and Q respectively are (2, 1, – 1) and (4, 4, – 7), is ______.
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk` and `3hati + 4hatk` form a triangle or not.
Check whether the vectors `2hati +2hatj+3hatk, -3hati +3hatj +2hatk and 3hati +4hatk` form a triangle or not.
Check whether the vectors `2hati + 2 hatj + 3hatk, - 3hati + 3hatj + 2hatk and 3hati + 4hatk` From a triangle or not.
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
