Advertisements
Advertisements
Question
Express the vector `bar"a" = 5hat"i" - 2hat"j" + 5hat"k"` as a sum of two vectors such that one is parallel to the vector `bar"b" = 3hat"i" + hat"k"` and other is perpendicular to `bar"b"`.
Solution
Let `bar"a" = bar"c" + bar"d"`, where `bar"c"` is parallel to `bar"b" and bar"d"` is perpendicular to `bar"b"`.
Since, `bar"c"` is parallel to `bar"b", bar"c" = "m"bar"b"`, where m is a scalar.
∴ `bar"c" = "m"(3hat"i" + hat"k")`
i.e. `bar"c" = 3"m"hat"i" + "m"hat"k"`
Let `bar"d" = "x"hat"i" + "y"hat"j"+ zhat"k"`
Since, `bar"d"` is perpendicular to `bar"b" = 3hat"i" + hat"k", bar"d".bar"b" = 0`
∴ `("x"hat"i" + "y"hat"j" + "z"hat"k").(3hat"i" + hat"k") = 0`
∴ 3x + z = 0
∴ z = - 3x
∴ `bar"d" = "x"hat"i" + "y"hat"k" - 3"x"hat"k"`
Now, `bar"a" = bar"c" + bar"d"` gives
∴ `5hat"i" - 2hat"j" + 5hat"k" = (3"m"hat"i" + "m"hat"k") + ("x"hat"i" + "y"hat"j" - 3"x"hat"k")`
`= (3"m" + "x")hat"i" + "y"hat"j" + ("m" - 3"x")hat"k"`
By equality of vectors
3m + x = 5 ....(1)
y = - 2
and m - 3x = 5 ......(2)
From (1) and (2)
3m + x = m - 3x
∴ 2m = - 4x
∴ m = - 2x
Substituting m = - 2x in (1), we get
∴ - 6x + x = 5
∴ - 5x = 5
∴ x = - 1
∴ m = - 2x = 2
∴ `bar"c" = 6hat"i" + 2hat"k"` is parallel to `bar"b" and bar"d" = - hat"i" - 2hat"j" + 3hat"k"` is perpendicular to `bar"b"`
Hence, `bar"a" = bar"c" + bar"d", "where" bar"c" = 6hat"i" + 2hat"k" and bar"d" = - hat"i" - 2hat"j" + 3hat"k"`
APPEARS IN
RELATED QUESTIONS
Write a unit vector making equal acute angles with the coordinates axes.
If a vector makes angles α, β, γ with OX, OY and OZ respectively, then write the value of sin2 α + sin2 β + sin2 γ.
If \[\overrightarrow{a} = \hat{i} + \hat{j} , \overrightarrow{b} = \hat{j} + \hat{k} , \overrightarrow{c} = \hat{k} + \hat{i}\], find the unit vector in the direction of \[\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}\].
If \[\overrightarrow{a} = x \hat{i} + 2 \hat{j} - z \hat{k}\text{ and }\overrightarrow{b} = 3 \hat{i} - y \hat{j} + \hat{k}\] are two equal vectors, then write the value of x + y + z.
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] and \[\vec{d}\] are the position vectors of points A, B, C, D such that no three of them are collinear and \[\vec{a} + \vec{c} = \vec{b} + \vec{d} ,\] then ABCD is a
Let G be the centroid of ∆ ABC. If \[\overrightarrow{AB} = \vec{a,} \overrightarrow{AC} = \vec{b,}\] then the bisector \[\overrightarrow{AG} ,\] in terms of \[\vec{a}\text{ and }\vec{b}\] is
If \[\vec{a}\text{ and }\vec{b}\] are two collinear vectors, then which of the following are incorrect?
Find the components along the coordinate axes of the position vector of the following point :
Q(–5, 1)
Find the value of λ for which the four points with position vectors `6hat"i" - 7hat"j", 16hat"i" - 19hat"j" - 4hat"k" , lambdahat"j" - 6hat"k" "and" 2hat"i" - 5hat"j" + 10hat"k"` are coplanar.
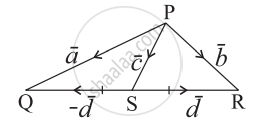
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Find the coordinates of the point which is located in the YZ-plane, one unit to the right of the XZ- plane, and six units above the XY-plane.
Find the area of the traingle with vertices (1, 1, 0), (1, 0, 1) and (0, 1, 1).
Select the correct option from the given alternatives:
If `bar"a" "and" bar"b"` are unit vectors, then what is the angle between `bar"a"` and `bar"b"` for `sqrt3bar"a" - bar"b"` to be a unit vector?
Select the correct option from the given alternatives:
If `bar"a", bar"b", bar"c"` are non-coplanar unit vectors such that `bar"a"xx (bar"b"xxbar"c") = (bar"b"+bar"c")/sqrt2`, then the angle between `bar"a" "and" bar"b"` is
Find the unit vectors that are parallel to the tangent line to the parabola y = x2 at the point (2, 4).
Let bar"b" = 4hat"i" + 3hat"j" and bar"c" be two vectors perpendicular to each other in the XY-plane. Find the vector in the same plane having projection 1 and 2 along bar"b" and bar"c" respectively.
Show that no line in space can make angles `pi/6` and `pi/4` with X-axis and Y-axis.
Find the angle between the lines whose direction cosines are given by the equations 6mn - 2nl + 5lm = 0, 3l + m + 5n = 0.
Show that the vector area of a triangle ABC, the position vectors of whose vertices are `bar"a", bar"b" and bar"c"` is `1/2[bar"a" xx bar"b" + bar"b" xx bar"c" + bar"c" xx bar"a"]`.
Find a unit vector perpendicular to the plane containing the point (a, 0, 0), (0, b, 0) and (0, 0, c). What is the area of the triangle with these vertices?
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a".(bar"b" xx bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a".(bar"b".bar"c")`
lf `overlinea` and `overlineb` be two unit vectors and θ is the angle between them, then `|overlinea - overlineb|` is equal to ______
For any vector `overlinex` the value of `(overlinex xx hati)^2 + (overlinex xx hatj)^2 + (overlinex xx hatk)^2` is equal to ______
lf `overlinea`, `overlineb` and `overlinec` are unit vectors such that `overlinea + overlineb + overlinec = overline0` and angle between `overlinea` and `overlineb` is `pi/3`, then `|overlinea xx overlineb| + |overlineb xx overlinec| + |overlinec xx overlinea|` = ______
The vector with initial point P (2, –3, 5) and terminal point Q(3, –4, 7) is ______.
If `vec"a" = hat"i" + hat"j" + 2hat"k"` and `vec"b" = 2hat"i" + hat"j" - 2hat"k"`, find the unit vector in the direction of `6vec"b"`
Classify the following measures as scalar and vector.
10-19 coulomb
Classify the following as scalar and vector quantity.
Velocity
Let `bara, barb` and `barc` be three vectors, then `bara xx (barb xx barc) = (bara xx barb) xx barc` if
The unit vector perpendicular to the vectors `6hati + 2hatj + 3hatk` and `3hati - 6hatj - 2hatk` is
In the triangle PQR, `bar(PQ) = 2bara` and `bar(QR)=2barb`. The mid-point of PR is M. Find following vectors in terms of `bar a and bar b `.
- `bar("PR")`
- `bar("PM")`
- `bar("QM")`
Check whether the vectors `2hati + 2hatj + 3hatk, - 3hati + 3hatj +2 hatk and 3hati + 4hatk` from a triangle or not.
Check whether the vectors `2hati + 2hatj + 3hat k, -3hati + 3hatj + 2hat k` and `3hati + 4hatk` form a triangle or not.
In the triangle PQR, `bar(PQ)=2bara` and `bar(QR)=2barb`. The mid-point of PR is M. Find following vectors in terms of `bara and barb`.
(i) `bar(PR)` (ii) `bar(PM)` (iii) `bar(QM)`
In the triangle PQR, `bar"PQ" = 2 bar" a" and bar"QR" = 2 bar"b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
