Advertisements
Advertisements
Question
If a parallelogram is constructed on the vectors `bar"a" = 3bar"p" - bar"q", bar"b" = bar"p" + 3bar"q" and |bar"p"| = |bar"q"| = 2` and angle between `bar"p" and bar"q"` is `pi/3,` and angle between lengths of the sides is `sqrt7 : sqrt13`.
Solution
`|bar"p"| = |bar"q"| = 2` and angle between `bar"p" and bar"q"` is `pi/3`.
∴ `bar"p".bar"q" = |bar"p"||bar"q"| "cos" pi/3 = 2xx2xx1/2 = 2`
Now, `bar"a" = 3bar"p" - bar"q"`
∴ `|bar"a"|^2 = |(3bar"p" - bar"q")|^2`
`= (3bar"p" - bar"q").(3bar"p" - bar"q")`
`= 3bar"p".(3bar"p" - bar"q") - bar"q".(3bar"p" - bar"q")`
`= 9bar"p".bar"p" - 3bar"p".bar"q" - 3bar"q".bar"p" + bar"q".bar"q"`
`= 9|bar"p"|^2 - 6bar"p".bar"q" + |bar"q"|^2` .....`[∵ bar"q".bar"p" = bar"p".bar"q"]`
`= 9xx4 - 6xx2 + 4 .......[∵ bar"p"bar"q" = 2]`
= 28
∴ `|bar"a"| = sqrt28`
Also `bar"b" = bar"p" + 3bar"q"`
∴ `|bar"b"|^2 = |bar"p" + 3bar"q"|^2`
`= (bar"p" + 3bar"q").(bar"p" + 3bar"q")`
`= bar"p"(bar"p" + 3bar"q") + 3bar"q"(bar"p" + 3bar"q")`
`= bar"p".bar"p" + 3bar"p".bar"q" - 3bar"q".bar"p" + 9bar"q".bar"q" ......[∵ bar"p".bar"q" = bar"q".bar"p"]`
`= |bar"p"|^2 + 3bar"p""q" + 3bar"p".bar"q" + 9 |bar"q"|^2`
= 4 + 12 + 36 ......`[∵ bar"p".bar"q" = 2]`
= 52
∴ `|bar"b"| = sqrt52`
Ratio of lengths of the sides
`= |bar"a"|/|bar"b"| = sqrt28/sqrt52 = (2sqrt7)/(2sqrt13) = sqrt7/sqrt13`.
Hence, the ratio of the lengths of the sides is `sqrt7 : sqrt13`.
APPEARS IN
RELATED QUESTIONS
Find the position vector of the mid-point of the line segment AB, where A is the point (3, 4, −2) and B is the point (1, 2, 4).
If` vec"a" = 2hat"i" + 3hat"j" + + hat"k", vec"b" = hat"i" - 2hat"j" + hat"k" "and" vec"c" = -3hat"i" + hat"j" + 2hat"k", "find" [vec"a" vec"b" vec"c"]`
The vector `bar"a"` is directed due north and `|bar"a"|` = 24. The vector `bar"b"` is directed due west and `|bar"b"| = 7`. Find `|bar"a" + bar"b"|`.
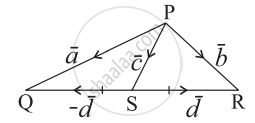
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Find the coordinates of the point which is located in the YZ-plane, one unit to the right of the XZ- plane, and six units above the XY-plane.
If the sum of two unit vectors is itself a unit vector, then the magnitude of their difference is ______.
Select the correct option from the given alternatives:
If `|bar"a"| = 3` and - 1 ≤ k ≤ 2, then `|"k"bar"a"|` lies in the interval
Select the correct option from the given alternatives:
Let α, β, γ be distinct real numbers. The points with position vectors `alphahat"i" + betahat"j" + gammahat"k", betahat"i" + gammahat"j" + alphahat"k", gammahat"i" + alphahat"j" + betahat"k"`
If `|bar"a"| = |bar"b"| = 1, bar"a".bar"b" = 0, bar"a" + bar"b" + bar"c" = bar"0", "find" |bar"c"|`.
Two sides of a parallelogram are `3hat"i" + 4hat"j" - 5hat"k"` and `-2hat"j" + 7hat"k"`. Find the unit vectors parallel to the diagonals.
A point P with position vector `(- 14hat"i" + 39hat"j" + 28hat"k")/5` divides the line joining A (1, 6, 5) and B in the ratio 3 : 2, then find the point B.
Let bar"b" = 4hat"i" + 3hat"j" and bar"c" be two vectors perpendicular to each other in the XY-plane. Find the vector in the same plane having projection 1 and 2 along bar"b" and bar"c" respectively.
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a" xx(bar"b" xx bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a".(bar"b" + bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a". bar"b" + bar"c"`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`|bar"a"|. (bar"b" + bar"c")`
If `bar"a", bar"b", bar"c"` are three non-coplanar vectors show that `(bar"a".(bar"b" xx bar"c"))/((bar"c" xx bar"a").bar"b") + (bar"b".(bar"a" xx bar"c"))/((bar"c" xx bar"a").bar"b") = 0`
If the vectors `overlinea = 2hati - qhatj + 3hatk` and `overlineb = 4hati - 5hatj + 6hatk` are collinear, then the value of q is ______
Using vectors, prove that cos (A – B) = cosA cosB + sinA sinB.
The vector with initial point P (2, –3, 5) and terminal point Q(3, –4, 7) is ______.
Find the unit vector in the direction of the sum of the vectors `vec"a" = 2hat"i" - hat"j" + hat"k"` and `vec"b" = 2hat"j" + hat"k"`.
Classify the following as scalar and vector quantity.
Force
Classify the following as scalar and vector quantity.
Work done
`bara, barb` and `barc` are three vectors such that `veca + vecb + vecc` 20, `|bara| = 1, |barb| = 2` and `|barc| = 3`. Then `bara. barb + barb.barc + bar(c.a)` is equal to
Four vectors `veca, vecb, vecc` and `vecx` satisfy the relation `(veca.vecx)vecb = vecc + vecx` where `vecb * veca` ≠ 1. The value of `vecx` in terms of `veca, vecb` and `vecc` is equal to
If points P(4, 5, x), Q(3, y, 4) and R(5, 8, 0) are collinear, then the value of x + y is ______.
Check whether the vectors `2hati +2hatj+3hatk, -3hati +3hatj +2hatk and 3hati +4hatk` form a triangle or not.
lf ΔABC is an equilateral triangle and length of each side is “a” units, then the value of `bar(AB)*bar(BC) + bar(BC)*bar(CA) + bar(CA)*bar(AB)` is ______.
Check whether the vectors `2hati + 2 hatj + 3hatk, - 3hati + 3hatj + 2hatk and 3hati + 4hatk` From a triangle or not.
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
In the triangle PQR, `bar(PQ)`= 2`bar a` and `bar(QR)`= 2`bar b` . The mid-point of PR is M. Find following vectors in terms of `bara` and `barb`.
- `bar(PR)`
- `bar(PM)`
- `bar(QM)`
In the triangle PQR, `bar(PQ) = 2bara and bar(QR) = 2barb`. The mid-point of PR is M. Find the following vectors in terms of `bara and barb`.
- `bar(PR)`
- `bar(PM)`
- `bar(QM)`
