Advertisements
Advertisements
Question
Find the unit vectors that are parallel to the tangent line to the parabola y = x2 at the point (2, 4).
Solution
Differentiating y =x2 w.r.t. x, we get `"dy"/"dx" = "2x"`
Slope of tangent at P(2, 4) = `("dy"/"dx")_("at""P"(2,4))` = 2 × 2 = 4
∴ the equation of tangent at P is
y - 4 = 4(x - 2)
∴ y = 4x - 4
∴ y = 4x is equation of line parallel to the tangent at P and passing through the origin O.
4x = y, z = 0
∴ `"x"/1 = "y"/4, "z" = 0`
∴ the direction ratios of this line are 1, 4, 0
∴ its direction cosines are
`+- 1/(sqrt(1^2 + 4^2 + 0^2)), +-4/sqrt(1^2 + 4^2 + 0^2), 0`
i.e. `+- 1/sqrt17, +-4/sqrt17, 0`
∴ unit vectors parallel to tangent line at P(2, 4) is
`+- 1/sqrt17(hat"i" + 4hat"j")`
APPEARS IN
RELATED QUESTIONS
If \[\vec{a}\] and \[\vec{b}\] are two non-collinear vectors such that \[x \vec{a} + y \vec{b} = \vec{0} ,\] then write the values of x and y.
If G denotes the centroid of ∆ABC, then write the value of \[\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} .\]
If a vector makes angles α, β, γ with OX, OY and OZ respectively, then write the value of sin2 α + sin2 β + sin2 γ.
Write the position vector of a point dividing the line segment joining points A and B with position vectors \[\vec{a}\] and \[\vec{b}\] externally in the ratio 1 : 4, where \[\overrightarrow{a} = 2 \hat{i} + 3 \hat{j} + 4 \hat{k} \text{ and }\overrightarrow{b} = - \hat{i} + \hat{j} + \hat{k} .\]
If \[\overrightarrow{a} = \hat{i} + 2 \hat{j} , \vec{b} = \hat{j} + 2 \hat{k} ,\] write a unit vector along the vector \[3 \overrightarrow{a} - 2 \overrightarrow{b} .\]
Write a unit vector in the direction of \[\overrightarrow{b} = 2 \hat{i} + \hat{j} + 2 \hat{k}\].
Write the position vector of the point which divides the join of points with position vectors \[3 \overrightarrow{a} - 2 \overrightarrow{b}\text{ and }2 \overrightarrow{a} + 3 \overrightarrow{b}\] in the ratio 2 : 1.
Let G be the centroid of ∆ ABC. If \[\overrightarrow{AB} = \vec{a,} \overrightarrow{AC} = \vec{b,}\] then the bisector \[\overrightarrow{AG} ,\] in terms of \[\vec{a}\text{ and }\vec{b}\] is
The position vectors of the points A, B, C are \[2 \hat{i} + \hat{j} - \hat{k} , 3 \hat{i} - 2 \hat{j} + \hat{k}\text{ and }\hat{i} + 4 \hat{j} - 3 \hat{k}\] respectively.
These points
Find the position vector of the mid-point of the vector joining the points
If `veca` and `vecb` are non- collinear vectors, find the value of x such that the vectors `barα = (x - 2)veca + vecb` and `barβ = (3+2x)bara - 2barb` are collinear.
Check whether the vectors `2hati + 2hatj + 3hatk, - 3hati + 3hatj + 2hatk` and `3hati + 4hatk` form a triangle or not.
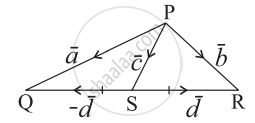
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Let `bara = hati - hatj, barb = hatj - hatk, barc = hatk - hati.` If `bard` is a unit vector such that `bara * bard = 0 = [(barb, barc, bard)]`, then `bard` equals ______.
Find the lengths of the sides of the triangle and also determine the type of a triangle:
L (3, -2, -3), M (7, 0, 1), N(1, 2, 1).
Two sides of a parallelogram are `3hat"i" + 4hat"j" - 5hat"k"` and `-2hat"j" + 7hat"k"`. Find the unit vectors parallel to the diagonals.
Find two unit vectors each of which makes equal angles with bar"u", bar"v" and bar"w" where bar"u" = 2hat"i" + hat"j" - 2hat"k", bar"v" = hat"i" + 2hat"j" - 2hat"k", bar"w" = 2hat"i" - 2hat"j" + hat"k".
Show that no line in space can make angles `pi/6` and `pi/4` with X-axis and Y-axis.
For any non zero vector, a, b, c a · ((b + c) × (a + b + c)] = ______.
If `vec"a" = 2hat"i" - hat"j" + hat"k", vec"b" = hat"i" + hat"j" - 2hat"k"` and `vec"c" = hat"i" + 3hat"j" - hat"k"`, find `lambda` such that `vec"a"` is perpendicular to `lambdavec"b" + vec"c"`.
The angle between the vectors `hat"i" - hat"j"` and `hat"j" - hat"k"` is ______.
The 2 vectors `hat"j" + hat"k"` and `3hat"i" - hat"j" + 4hat"k"` represents the two sides AB and AC, respectively of a ∆ABC. The length of the median through A is ______.
Using vectors, find the value of k such that the points (k, – 10, 3), (1, –1, 3) and (3, 5, 3) are collinear.
The formula `(vec"a" + vec"b")^2 = vec"a"^2 + vec"b"^2 + 2vec"a" xx vec"b"` is valid for non-zero vectors `vec"a"` and `vec"b"`
Classify the following measures as scalar and vector.
20 m/s2
Classify the following as scalar and vector quantity.
Work done
Four vectors `veca, vecb, vecc` and `vecx` satisfy the relation `(veca.vecx)vecb = vecc + vecx` where `vecb * veca` ≠ 1. The value of `vecx` in terms of `veca, vecb` and `vecc` is equal to
Find `|vecx|`, if for a unit vector `veca, (vecx - veca) * (vecx + veca)` = 12
Let the vectors `vec(a)` such `vec(b)` that `|veca|` = 3 and `|vecb| = sqrt(2)/3`, then `veca xx vecb` is a unit vector if the angle between `veca` and `vecb` is
If `veca = hati - hatj + 7hatk` and `vecb = 5hati - hatj + λhatk`, then find the value of λ so that the vectors `veca + vecb` and `veca - vecb` are orthogonal.
If A(1, 2, – 3) and B(– 1, – 2, 1) are the end points of a vector `vec("AB")` then find the unit vector in the direction of `vec("AB")`.
lf ΔABC is an equilateral triangle and length of each side is “a” units, then the value of `bar(AB)*bar(BC) + bar(BC)*bar(CA) + bar(CA)*bar(AB)` is ______.
In the triangle PQR, `bar"PQ" = bar"2a", bar"QR" = bar"2b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`.
Check whether the vectors `2hati + 2hatj +3hatk, - 3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
In the triangle PQR, `bar(PQ)`= 2`bar a` and `bar(QR)`= 2`bar b` . The mid-point of PR is M. Find following vectors in terms of `bara` and `barb`.
- `bar(PR)`
- `bar(PM)`
- `bar(QM)`
