Advertisements
Advertisements
Question
Find a unit vector in the direction of `vec"PQ"`, where P and Q have co-ordinates (5, 0, 8) and (3, 3, 2), respectively
Solution
Given coordinates are P(5, 0, 8) and Q(3, 3, 2)
∴ `vec"PQ"` = `(3 - 5)hat"i" + (3 - 0)hat"j" + (2 - 8)hat"k"`
= `-2hat"i" + 3hat"j" - 6hat"k"`
∴ Unit vector in the direction of `vec"PQ" = vec"PQ"/|vec"PQ"|`
= `(-2hat"i" + 3hat"j" - 6hat"k")/sqrt((-2)^2 + (3)^2 + (-6)^2)`
= `(-2hat"i" + 3hat"j" - 6hat"k")/sqrt(4 + 9 + 36)`
= `(-2hat"i" + 3hat"j" - 6hat"k")/sqrt(49)`
= `(-2hat"i" + 3hat"j" - 6hat"k")/7`
= `1/7 (-2hat"i" + 3hat"j" - 6hat"k")`
Hence, the required unit vector is `1/7 (-2hat"i" + 3hat"j" - 6hat"k")`.
APPEARS IN
RELATED QUESTIONS
If \[\vec{a}\] and \[\vec{b}\] are two non-collinear vectors such that \[x \vec{a} + y \vec{b} = \vec{0} ,\] then write the values of x and y.
Write a unit vector making equal acute angles with the coordinates axes.
Write a unit vector in the direction of \[\overrightarrow{a} = 3 \hat{i} + 2 \hat{j} + 6 \hat{k} .\]
Write a unit vector in the direction of \[\overrightarrow{b} = 2 \hat{i} + \hat{j} + 2 \hat{k}\].
Find a unit vector in the direction of \[\overrightarrow{a} = 2 \hat{i} - 3 \hat{j} + 6 \hat{k}\].
Find a unit vector in the direction of the vector \[\overrightarrow{a} = 3 \hat{i} - 2 \hat{j} + 6 \hat{k}\].
Forces 3 O \[\vec{A}\], 5 O \[\vec{B}\] act along OA and OB. If their resultant passes through C on AB, then
Let G be the centroid of ∆ ABC. If \[\overrightarrow{AB} = \vec{a,} \overrightarrow{AC} = \vec{b,}\] then the bisector \[\overrightarrow{AG} ,\] in terms of \[\vec{a}\text{ and }\vec{b}\] is
If three points A, B and C have position vectors \[\hat{i} + x \hat{j} + 3 \hat{k} , 3 \hat{i} + 4 \hat{j} + 7 \hat{k}\text{ and }y \hat{i} - 2 \hat{j} - 5 \hat{k}\] respectively are collinear, then (x, y) =
Check whether the vectors `2hati + 2hatj + 3hatk, - 3hati + 3hatj + 2hatk` and `3hati + 4hatk` form a triangle or not.
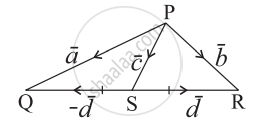
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Select the correct option from the given alternatives:
If `|bar"a"| = 3` and - 1 ≤ k ≤ 2, then `|"k"bar"a"|` lies in the interval
Dot product of a vector with vectors `3hat"i" - 5hat"k", 2hat"i" + 7hat"j" and hat"i" + hat"j" + hat"k"` are respectively -1, 6 and 5. Find the vector.
Find two unit vectors each of which makes equal angles with bar"u", bar"v" and bar"w" where bar"u" = 2hat"i" + hat"j" - 2hat"k", bar"v" = hat"i" + 2hat"j" - 2hat"k", bar"w" = 2hat"i" - 2hat"j" + hat"k".
If A, B, C and D are (3, 7, 4), (5, -2, - 3), (- 4, 5, 6) and(1, 2, 3) respectively, then the volume of the parallelopiped with AB, AC and AD as the co-terminus edges, is ______ cubic units.
For 0 < θ < π, if A = `[(costheta, -sintheta), (sintheta, costheta)]`, then ______
Find a vector `vec"r"` of magnitude `3sqrt(2)` units which makes an angle of `pi/4` and `pi/2` with y and z-axes, respectively.
If `|vec"a"|` = 3 and –1 ≤ k ≤ 2, then `|"k"vec"a"|` lies in the interval ______.
If `vec"a", vec"b", vec"c"` determine the vertices of a triangle, show that `1/2[vec"b" xx vec"c" + vec"c" xx vec"a" + vec"a" xx vec"b"]` gives the vector area of the triangle. Hence deduce the condition that the three points `vec"a", vec"b", vec"c"` are collinear. Also find the unit vector normal to the plane of the triangle.
If `vec"a", vec"b", vec"c"` are unit vectors such that `vec"a" + vec"b" + vec"c"` = 0, then the value of `vec"a" * vec"b" + vec"b" * vec"c" + vec"c" * vec"a"` is ______.
Classify the following measures as scalar and vector.
2 meters north-west
If `veca ≠ vec(0), veca.vecb = veca.vecc, veca xx vecb = veca xx vecc`, then show that `vecb = vecc`.
For given vectors, `veca = 2hati - hatj + 2hatk` and `vecb = - hati + hatj - hatk` find the unit vector in the direction of the vector `veca + vecb`.
Let the vectors `vec(a)` such `vec(b)` that `|veca|` = 3 and `|vecb| = sqrt(2)/3`, then `veca xx vecb` is a unit vector if the angle between `veca` and `vecb` is
Check whether the vectors `2hati + 2hatj + 3hat k, -3hati + 3hatj + 2hat k` and `3hati + 4hatk` form a triangle or not.
In the triangle PQR, `bb(bar(PQ) = 2 bara)` and `bb(bar(QR) = 2 barb)`. The mid-point of PR is M. Find the following vectors in terms of `bb(bara and barb)`.
- `bar(PR)`
- `bar(PM)`
- `bar(QM)`
Check whether the vectors `2hati+2hatj+3hatk,-3hati+3hatj+2hatk` and `3hati+4hatk` form a triangle or not.
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
