Advertisements
Advertisements
Question
Classify the following measures as scalar and vector.
2 meters north-west
Solution
2 meters north-west is a vector quantity as it involves both magnitude and direction.
APPEARS IN
RELATED QUESTIONS
If `veca=xhati+2hatj-zhatk and vecb=3hati-yhatj+hatk` are two equal vectors ,then write the value of x+y+z
If \[\vec{a}\] and \[\vec{b}\] are two non-collinear vectors such that \[x \vec{a} + y \vec{b} = \vec{0} ,\] then write the values of x and y.
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] are the position vectors of the vertices of an equilateral triangle whose orthocentre is at the origin, then write the value of \[\vec{a} + \vec{b} + \vec{c} .\]
Write a unit vector in the direction of \[\overrightarrow{a} = 3 \hat{i} + 2 \hat{j} + 6 \hat{k} .\]
Write a unit vector in the direction of \[\overrightarrow{b} = 2 \hat{i} + \hat{j} + 2 \hat{k}\].
Find a unit vector in the direction of \[\overrightarrow{a} = 2 \hat{i} - 3 \hat{j} + 6 \hat{k}\].
Find a unit vector in the direction of the vector \[\overrightarrow{a} = 3 \hat{i} - 2 \hat{j} + 6 \hat{k}\].
If \[\left| \overrightarrow{a} \right| = 4\] and \[- 3 \leq \lambda \leq 2\], then write the range of \[\left| \lambda \vec{a} \right|\].
If \[\vec{a} , \vec{b}\] are the vectors forming consecutive sides of a regular hexagon ABCDEF, then the vector representing side CD is
If points A (60 \[\hat{i}\] + 3 \[\hat{j}\]), B (40 \[\hat{i}\] − 8 \[\hat{j}\]) and C (a \[\hat{i}\] − 52 \[\hat{j}\]) are collinear, then a is equal to
Let G be the centroid of ∆ ABC. If \[\overrightarrow{AB} = \vec{a,} \overrightarrow{AC} = \vec{b,}\] then the bisector \[\overrightarrow{AG} ,\] in terms of \[\vec{a}\text{ and }\vec{b}\] is
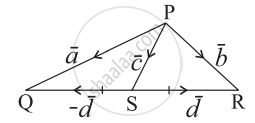
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Find the coordinates of the point which is located three units behind the YZ-plane, four units to the right of XZ-plane, and five units above the XY-plane.
Let `bara = hati - hatj, barb = hatj - hatk, barc = hatk - hati.` If `bard` is a unit vector such that `bara * bard = 0 = [(barb, barc, bard)]`, then `bard` equals ______.
Select the correct option from the given alternatives:
If `bar"a", bar"b", bar"c"` are non-coplanar unit vectors such that `bar"a"xx (bar"b"xxbar"c") = (bar"b"+bar"c")/sqrt2`, then the angle between `bar"a" "and" bar"b"` is
If a parallelogram is constructed on the vectors `bar"a" = 3bar"p" - bar"q", bar"b" = bar"p" + 3bar"q" and |bar"p"| = |bar"q"| = 2` and angle between `bar"p" and bar"q"` is `pi/3,` and angle between lengths of the sides is `sqrt7 : sqrt13`.
Find the angle between the lines whose direction cosines are given by the equations 6mn - 2nl + 5lm = 0, 3l + m + 5n = 0.
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a" xx(bar"b" xx bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a". bar"b" + bar"c"`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`|bar"a"|. (bar"b" + bar"c")`
If the vectors `xhat"i" - 3hat"j" + 7hat"k" and hat"i" + "y"hat"j" - "z"hat"k"` are collinear then the value of `"xy"^2/"z"` is equal.
a and b are non-collinear vectors. If c = (x - 2)a + b and d = (2x + 1)a - b are collinear vectors, then the value of x = ______.
Find the unit vector in the direction of the sum of the vectors `vec"a" = 2hat"i" - hat"j" + 2hat"k"` and `vec"b" = -hat"i" + hat"j" + 3hat"k"`.
Find the unit vector in the direction of the sum of the vectors `vec"a" = 2hat"i" - hat"j" + hat"k"` and `vec"b" = 2hat"j" + hat"k"`.
Find a unit vector in the direction of `vec"PQ"`, where P and Q have co-ordinates (5, 0, 8) and (3, 3, 2), respectively
If `vec"a", vec"b", vec"c"` determine the vertices of a triangle, show that `1/2[vec"b" xx vec"c" + vec"c" xx vec"a" + vec"a" xx vec"b"]` gives the vector area of the triangle. Hence deduce the condition that the three points `vec"a", vec"b", vec"c"` are collinear. Also find the unit vector normal to the plane of the triangle.
If `vec"a"` is any non-zero vector, then `(vec"a" .hat"i")hat"i" + (vec"a".hat"j")hat"j" + (vec"a".hat"k")hat"k"` equals ______.
Classify the following as scalar and vector quantity.
Distance
Classify the following as scalar and vector quantity.
Force
In Figure, identify the following vector.

Equal
Find `|vecx|`, if for a unit vector `veca, (vecx - veca) * (vecx + veca)` = 12
Let the vectors `vec(a)` such `vec(b)` that `|veca|` = 3 and `|vecb| = sqrt(2)/3`, then `veca xx vecb` is a unit vector if the angle between `veca` and `vecb` is
If `veca = hati - hatj + 7hatk` and `vecb = 5hati - hatj + λhatk`, then find the value of λ so that the vectors `veca + vecb` and `veca - vecb` are orthogonal.
If points P(4, 5, x), Q(3, y, 4) and R(5, 8, 0) are collinear, then the value of x + y is ______.
Check whether the vectors`2hati+2hatj+3hatk,-3hati+3hatj+2hatk and 3hati +4hatk` form a triangle or not.
In the triangle PQR, `bar(PQ)` = 2`bara` and `bar(QR)` = 2`barb`. The mid-point of PR is M. Find following vectors in terms of `bara` and `barb`.
- `bar(PR)`
- `bar(PM)`
- `bar(QM)`
Check whether the vectors `2hati + 2 hatj + 3hatk, - 3hati + 3hatj + 2hatk and 3hati + 4hatk` From a triangle or not.
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
