Advertisements
Advertisements
Question
If three points A, B and C have position vectors \[\hat{i} + x \hat{j} + 3 \hat{k} , 3 \hat{i} + 4 \hat{j} + 7 \hat{k}\text{ and }y \hat{i} - 2 \hat{j} - 5 \hat{k}\] respectively are collinear, then (x, y) =
Options
(2, −3)
(−2, 3)
(−2, −3)
(2, 3)
Solution
(2, −3)
Given position vectors of A, B and C are \[\hat{i} + x \hat{j} + 3 \hat{k} , 3 \hat{i} + 4 \hat{j} + 7 \hat{k}\] and \[y \hat{i} - 2 \hat{j} - 5 \hat{k} .\]
Then,
\[\overrightarrow{AB} = 3 \hat{i} + 4 \hat{j} + 7 \hat{k} - \hat{i} - x \hat{j} - 3 \hat{k} = 2 \hat{i} + \left( 4 - x \right) \hat{j} + 4 \hat{k} \]
\[ \overrightarrow{BC} = y \hat{i} - 2 \hat{j} - 5 \hat{k} - 3 \hat{i} - 4 \hat{j} - 7 \hat{k} = \left( y - 3 \right) \hat{i} - 6 \hat{j} - 12 \hat{k}\]
Since, the given vectors are collinear.
\[\therefore \overrightarrow{AB} = \lambda \overrightarrow{BC} \]
\[ \Rightarrow 2 \hat{i} + \left( 4 - x \right) \hat{j} + 4 \hat{k} = \lambda \left( y - 3 \right) \hat{i} - 6\lambda \hat{j} - 12\lambda \hat{k} \]
\[ \Rightarrow 2 = \lambda \left( y - 3 \right) , \left( 4 - x \right) = - 6\lambda, 4 = - 12\lambda \]
\[ \Rightarrow 2 = \lambda \left( y - 3 \right) , \left( 4 - x \right) = - 6\lambda, \lambda = - \frac{1}{3}\]
\[ \Rightarrow 2 = - \frac{1}{3}\left( y - 3 \right) , \left( 4 - x \right) = - 6 \times \left( - \frac{1}{3} \right)\]
\[ \Rightarrow - 6 = y - 3 , 4 - x = 2\]
\[ \Rightarrow y = - 3 , x = 2\]
APPEARS IN
RELATED QUESTIONS
If `veca=xhati+2hatj-zhatk and vecb=3hati-yhatj+hatk` are two equal vectors ,then write the value of x+y+z
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] are position vectors of the vertices A, B and C respectively, of a triangle ABC, write the value of \[\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CA} .\]
If D, E, F are the mid-points of the sides BC, CA and AB respectively of a triangle ABC, write the value of \[\overrightarrow{AD} + \overrightarrow{BE} + \overrightarrow{CF} .\]
Write the position vector of a point dividing the line segment joining points having position vectors \[\hat{i} + \hat{j} - 2 \hat{k} \text{ and }2 \hat{i} - \hat{j} + 3 \hat{k}\] externally in the ratio 2:3.
Find the position vector of the mid-point of the line segment AB, where A is the point (3, 4, −2) and B is the point (1, 2, 4).
For what value of 'a' the vectors \[2 \hat{i} - 3 \hat{j} + 4 \hat{k} \text{ and }a \hat{i} + 6 \hat{j} - 8 \hat{k}\] are collinear?
Write a unit vector in the direction of \[\overrightarrow{PQ}\], where P and Q are the points (1, 3, 0) and (4, 5, 6) respectively.
If \[\vec{a} , \vec{b} , \vec{c}\] are three non-zero vectors, no two of which are collinear and the vector \[\vec{a} + \vec{b}\] is collinear with \[\vec{c} , \vec{b} + \vec{c}\] is collinear with \[\vec{a} ,\] then \[\vec{a} + \vec{b} + \vec{c} =\]
The position vectors of the points A, B, C are \[2 \hat{i} + \hat{j} - \hat{k} , 3 \hat{i} - 2 \hat{j} + \hat{k}\text{ and }\hat{i} + 4 \hat{j} - 3 \hat{k}\] respectively.
These points
Find the components along the coordinate axes of the position vector of the following point :
R(–11, –9)
Find a unit vector perpendicular to each of the vectors `veca + vecb "and" veca - vecb "where" veca = 3hati + 2hatj + 2hatk and vecb = i + 2hatj - 2hatk`
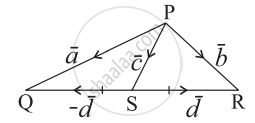
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Find a vector in the direction of `bara = hati - 2hatj` that has magnitude 7 units.
If the sum of two unit vectors is itself a unit vector, then the magnitude of their difference is ______.
If `|bara|` = 3, `|barb|` = 5, `|barc|` = 7 and `bara + barb + barc = bar0`, then the angle between `bara` and `barb` is ______.
Find the lengths of the sides of the triangle and also determine the type of a triangle:
A(2, -1, 0), B(4, 1, 1), C(4, -5, 4)
A point P with position vector `(- 14hat"i" + 39hat"j" + 28hat"k")/5` divides the line joining A (1, 6, 5) and B in the ratio 3 : 2, then find the point B.
Find two unit vectors each of which makes equal angles with bar"u", bar"v" and bar"w" where bar"u" = 2hat"i" + hat"j" - 2hat"k", bar"v" = hat"i" + 2hat"j" - 2hat"k", bar"w" = 2hat"i" - 2hat"j" + hat"k".
Show that no line in space can make angles `pi/6` and `pi/4` with X-axis and Y-axis.
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a" xx(bar"b" xx bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`(bar"a".bar"b").bar"c"`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`|bar"a"|. (bar"b" + bar"c")`
The vector eqliation of line 2x - 2 = 3y + 1 = 6z - 2 is
lf `overlinea` and `overlineb` be two unit vectors and θ is the angle between them, then `|overlinea - overlineb|` is equal to ______
If the vectors `overlinea = 2hati - qhatj + 3hatk` and `overlineb = 4hati - 5hatj + 6hatk` are collinear, then the value of q is ______
Find a vector `vec"r"` of magnitude `3sqrt(2)` units which makes an angle of `pi/4` and `pi/2` with y and z-axes, respectively.
Using vectors, prove that cos (A – B) = cosA cosB + sinA sinB.
The area of the parallelogram whose adjacent sides are `hat"i" + hat"k"` and `2hat"i" + hat"j" + hat"k"` is ______.
The formula `(vec"a" + vec"b")^2 = vec"a"^2 + vec"b"^2 + 2vec"a" xx vec"b"` is valid for non-zero vectors `vec"a"` and `vec"b"`
Let `veca, vecb` and `vecc` be three unit vectors such that `veca xx (vecb xx vecc) = sqrt(3)/2 (vecb + vecc)`. If `vecb` is not parallel to `vecc`, then the angle between `veca` and `vecc` is
`bara, barb` and `barc` are three vectors such that `veca + vecb + vecc` 20, `|bara| = 1, |barb| = 2` and `|barc| = 3`. Then `bara. barb + barb.barc + bar(c.a)` is equal to
For given vectors, `veca = 2hati - hatj + 2hatk` and `vecb = - hati + hatj - hatk` find the unit vector in the direction of the vector `veca + vecb`.
Find `|vecx|`, if for a unit vector `veca, (vecx - veca) * (vecx + veca)` = 12
Find `|veca xx vecb|`, if `veca = hati - 7hatj + 7hatk` and `vecb = 3hati - 2hatj + 2hatk`
In the triangle PQR, `bar("P""Q")`= `2 bar"a"` and `bar ("QR")` = `2 barb`.The mid - point of PR is M. Find following vector in term of `bar a ` and `barb.`
- `bar("P""R")`
- `bar("P""M")`
- `bar("Q""M")`
Check whether the vectors `2hati + 2hatj + 3hat k, -3hati + 3hatj + 2hat k` and `3hati + 4hatk` form a triangle or not.
In the triangle PQR, `bb(bar(PQ) = 2 bara)` and `bb(bar(QR) = 2 barb)`. The mid-point of PR is M. Find the following vectors in terms of `bb(bara and barb)`.
- `bar(PR)`
- `bar(PM)`
- `bar(QM)`
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
