Advertisements
Advertisements
Question
For what value of 'a' the vectors \[2 \hat{i} - 3 \hat{j} + 4 \hat{k} \text{ and }a \hat{i} + 6 \hat{j} - 8 \hat{k}\] are collinear?
Solution
Given: Two vectors , let \[\overrightarrow{p} =\] \[2 \hat{i} - 3 \hat{j} + 4 \hat{k}\] and \[\overrightarrow{q} =\] \[a \hat{i} + 6 \hat{j} - 8 \hat{k}\]
Since the given vectors are collinear, we have, \[\overrightarrow{p} = \lambda \overrightarrow{q}\]
\[\Rightarrow 2 \hat{i} - 3 \hat{j} + 4 \hat{k} = \lambda \left( a \hat{i} + 6 \hat{j} - 8 \hat{k} \right)\]
\[ \Rightarrow 2 \hat{i} - 3 \hat{j} + 4 \hat{k} = a\lambda \hat{i} + 6\lambda \hat{j} - 8\lambda \hat{k} \]
\[\Rightarrow \lambda a = 2, 6\lambda = - 3\text{ and }- 8\lambda = 4\]
\[ \Rightarrow \lambda = - \frac{1}{2}\text{ and }a = - 4\]
APPEARS IN
RELATED QUESTIONS
If \[\vec{a}\] and \[\vec{b}\] represent two adjacent sides of a parallelogram, then write vectors representing its diagonals.
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] are position vectors of the vertices A, B and C respectively, of a triangle ABC, write the value of \[\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CA} .\]
If a vector makes angles α, β, γ with OX, OY and OZ respectively, then write the value of sin2 α + sin2 β + sin2 γ.
If \[\overrightarrow{a} = x \hat{i} + 2 \hat{j} - z \hat{k}\text{ and }\overrightarrow{b} = 3 \hat{i} - y \hat{j} + \hat{k}\] are two equal vectors, then write the value of x + y + z.
Find the value of 'p' for which the vectors \[3 \hat{i} + 2 \hat{j} + 9 \hat{k}\] and \[\hat{i} - 2p \hat{j} + 3 \hat{k}\] are parallel.
In a triangle OAC, if B is the mid-point of side AC and \[\overrightarrow{OA} = \overrightarrow{a} , \overrightarrow{OB} = \overrightarrow{b}\], then what is \[\overrightarrow{OC}\].
Forces 3 O \[\vec{A}\], 5 O \[\vec{B}\] act along OA and OB. If their resultant passes through C on AB, then
If points A (60 \[\hat{i}\] + 3 \[\hat{j}\]), B (40 \[\hat{i}\] − 8 \[\hat{j}\]) and C (a \[\hat{i}\] − 52 \[\hat{j}\]) are collinear, then a is equal to
Let G be the centroid of ∆ ABC. If \[\overrightarrow{AB} = \vec{a,} \overrightarrow{AC} = \vec{b,}\] then the bisector \[\overrightarrow{AG} ,\] in terms of \[\vec{a}\text{ and }\vec{b}\] is
In the triangle PQR, `bar"PQ" = bar"2a", bar"QR" = bar"2b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`.
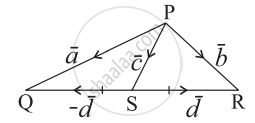
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Find the coordinates of the point which is located three units behind the YZ-plane, four units to the right of XZ-plane, and five units above the XY-plane.
If the sum of two unit vectors is itself a unit vector, then the magnitude of their difference is ______.
Select the correct option from the given alternatives:
Let a, b, c be distinct non-negative numbers. If the vectors `"a"hat"i" + "a"hat"j" + "c"hat"k" , hat"i" + hat"k" "and" "c"hat"i" + "c"hat"j" + "b"hat"k"` lie in a plane, then c is
Find the component form of `bar"a"` if it lies in YZ-plane makes 60° with positive Y-axis and `|bar"a"| = 4`.
ABCD is a parallelogram. E, F are the midpoints of BC and CD respectively. AE, AF meet the diagonal BD at Q and P respectively. Show that P and Q trisect DB.
Show that no line in space can make angles `pi/6` and `pi/4` with X-axis and Y-axis.
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a" xx(bar"b" xx bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a".(bar"b".bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`|bar"a"|. (bar"b" + bar"c")`
For any non-zero vectors a and b, [b a × b a] = ?
a and b are non-collinear vectors. If c = (x - 2)a + b and d = (2x + 1)a - b are collinear vectors, then the value of x = ______.
For any non zero vector, a, b, c a · ((b + c) × (a + b + c)] = ______.
If the vectors `overlinea = 2hati - qhatj + 3hatk` and `overlineb = 4hati - 5hatj + 6hatk` are collinear, then the value of q is ______
The 2 vectors `hat"j" + hat"k"` and `3hat"i" - hat"j" + 4hat"k"` represents the two sides AB and AC, respectively of a ∆ABC. The length of the median through A is ______.
Classify the following measures as scalar and vector.
20 m/s2
Classify the following as scalar and vector quantity.
Work done
In Figure, identify the following vector.

Equal
If `veca ≠ vec(0), veca.vecb = veca.vecc, veca xx vecb = veca xx vecc`, then show that `vecb = vecc`.
Which of the following measures as vector?
Check whether the vectors `2hati + 2hatj + 3hat k, -3hati + 3hatj + 2hat k` and `3hati + 4hatk` form a triangle or not.
If `hata` is unit vector and `(2vecx - 3hata)*(2vecx + 3hata)` = 91, find the value of `|vecx|`.
In the triangle PQR, `bar(PQ)=2bara` and `bar(QR)=2barb`. The mid-point of PR is M. Find following vectors in terms of `bara and barb`.
(i) `bar(PR)` (ii) `bar(PM)` (iii) `bar(QM)`
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
Check whether the vectors `2hati + 2hatj +3hatk, - 3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
