Advertisements
Advertisements
प्रश्न
If O and O' are circumcentre and orthocentre of ∆ ABC, then \[\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC}\] equals
पर्याय
2\[\overrightarrow{OO}\]
- \[O \overrightarrow{O'}\]
- \[\overrightarrow{OO'}\]
- \[2 \overrightarrow{O'O}\]
उत्तर
Given: O be the circumcentre and \[O'\] be the orthocentre of \[\bigtriangleup ABC\].
Let G be the centroid of the triangle.
We know that O, G and H are collinear and by geometry \[\overrightarrow{O'G} = 2 \overrightarrow{OG} .\]
This yields, \[\overrightarrow{O'O} = \overrightarrow{O'G} + \overrightarrow{GO} = 2 \overrightarrow{GO} + \overrightarrow{GO} = 3 \overrightarrow{GO} . \]
In other words \[\overrightarrow{OO'} = 3 \overrightarrow{OG} .\]
Since, \[\overrightarrow{OG} = \frac{\vec{a} + \vec{b} + \vec{c}}{3}\]
∴ \[\overrightarrow{OO'} = 3 \times \frac{\vec{a} + \vec{b} + \vec{c}}{3} = \vec{a} + \vec{b} + \vec{c} = \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} .\]
APPEARS IN
संबंधित प्रश्न
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] represent the sides of a triangle taken in order, then write the value of \[\vec{a} + \vec{b} + \vec{c} .\]
If \[\overrightarrow{a} = \hat{i} + \hat{j} , \vec{b} = \hat{j} + \hat{k} \text{ and }\vec{c} = \hat{k} + \hat{i} ,\] write unit vectors parallel to \[\overrightarrow{a} + \overrightarrow{b} - 2 \overrightarrow{c} .\]
If \[\overrightarrow{a} = \hat{i} + 2 \hat{j} - 3 \hat{k} \text{ and }\overrightarrow{b} = 2 \hat{i} + 4 \hat{j} + 9 \hat{k} ,\] find a unit vector parallel to \[\overrightarrow{a} + \overrightarrow{b}\].
Write a unit vector in the direction of \[\overrightarrow{b} = 2 \hat{i} + \hat{j} + 2 \hat{k}\].
If \[\vec{a} , \vec{b} , \vec{c}\] are three non-zero vectors, no two of which are collinear and the vector \[\vec{a} + \vec{b}\] is collinear with \[\vec{c} , \vec{b} + \vec{c}\] is collinear with \[\vec{a} ,\] then \[\vec{a} + \vec{b} + \vec{c} =\]
If points A (60 \[\hat{i}\] + 3 \[\hat{j}\]), B (40 \[\hat{i}\] − 8 \[\hat{j}\]) and C (a \[\hat{i}\] − 52 \[\hat{j}\]) are collinear, then a is equal to
If \[\vec{a}\text{ and }\vec{b}\] are two collinear vectors, then which of the following are incorrect?
If `veca` and `vecb` are non- collinear vectors, find the value of x such that the vectors `barα = (x - 2)veca + vecb` and `barβ = (3+2x)bara - 2barb` are collinear.
OABCDE is a regular hexagon. The points A and B have position vectors `bar"a"` and `bar"b"` respectively referred to the origin O. Find, in terms of `bar"a"` and `bar"b"` the position vectors of C, D and E.
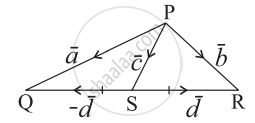
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Find the distance from (4, - 2, 6) to each of the following:
(a) The XY-plane
(b) The YZ-plane
(c) The XZ-plane
(d) The X-axis
(e) The Y-axis
(f) The Z-axis.
If two sides of a triangle are `hat"i" + 2hat"j" and hat"i" + hat"k"`, find the length of the third side.
Find the lengths of the sides of the triangle and also determine the type of a triangle:
A(2, -1, 0), B(4, 1, 1), C(4, -5, 4)
Find the component form of `bar"a"` if it lies in YZ-plane makes 60° with positive Y-axis and `|bar"a"| = 4`.
Let bar"b" = 4hat"i" + 3hat"j" and bar"c" be two vectors perpendicular to each other in the XY-plane. Find the vector in the same plane having projection 1 and 2 along bar"b" and bar"c" respectively.
Find the angle between the lines whose direction cosines are given by the equations 6mn - 2nl + 5lm = 0, 3l + m + 5n = 0.
Find a unit vector perpendicular to the plane containing the point (a, 0, 0), (0, b, 0) and (0, 0, c). What is the area of the triangle with these vertices?
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a".(bar"b" xx bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a".(bar"b" + bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`|bar"a"|. (bar"b" + bar"c")`
For any vectors `bar"a", bar"b", bar"c"` show that `(bar"a" + bar"b" + bar"c") xx bar"c" + (bar"a" + bar"b" + bar"c") xx bar"b" + (bar"b" - bar"c") xx bar"a" = 2bar"a" xx bar"c"`
For 0 < θ < π, if A = `[(costheta, -sintheta), (sintheta, costheta)]`, then ______
lf `overlinea`, `overlineb` and `overlinec` are unit vectors such that `overlinea + overlineb + overlinec = overline0` and angle between `overlinea` and `overlineb` is `pi/3`, then `|overlinea xx overlineb| + |overlineb xx overlinec| + |overlinec xx overlinea|` = ______
Using vectors, prove that cos (A – B) = cosA cosB + sinA sinB.
If `veca` and `vecb` are unit vectors, then what is the angle between `veca` and `vecb` for `sqrt(3) veca - vecb` to be a unit vector?
The unit vector perpendicular to the vectors `hat"i" - hat"j"` and `hat"i" + hat"j"` forming a right handed system is ______.
If `vec"a" = hat"i" + hat"j" + 2hat"k"` and `hat"b" = 2hat"i" + hat"j" - 2hat"k"`, find the unit vector in the direction of `2vec"a" - vec"b"`
Classify the following as scalar and vector quantity.
Force
Classify the following as scalar and vector quantity.
Work done
`bara, barb` and `barc` are three vectors such that `veca + vecb + vecc` 20, `|bara| = 1, |barb| = 2` and `|barc| = 3`. Then `bara. barb + barb.barc + bar(c.a)` is equal to
If `veca = hati - hatj + 7hatk` and `vecb = 5hati - hatj + λhatk`, then find the value of λ so that the vectors `veca + vecb` and `veca - vecb` are orthogonal.
If `hata` is unit vector and `(2vecx - 3hata)*(2vecx + 3hata)` = 91, find the value of `|vecx|`.
lf ΔABC is an equilateral triangle and length of each side is “a” units, then the value of `bar(AB)*bar(BC) + bar(BC)*bar(CA) + bar(CA)*bar(AB)` is ______.
Check whether the vectors `2hati + 2 hatj + 3hatk, - 3hati + 3hatj + 2hatk and 3hati + 4hatk` From a triangle or not.
Evaluate the following.
`int x^3/(sqrt1 + x^4) `dx
Consider the following statements and choose the correct option:
Statement 1: If `veca` and `vecb` represents two adjacent sides of a parallelogram then the diagonals are represented by `veca + vecb` and `veca - vecb`.
Statement 2: If `veca` and `vecb` represents two diagonals of a parallelogram then the adjacent sides are represented by `2(veca + vecb)` and `2(veca - vecb)`.
Which of the following is correct?
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
