Advertisements
Advertisements
Question
If G is the intersection of diagonals of a parallelogram ABCD and O is any point, then \[O \vec{A} + O \vec{B} + O \vec{C} + O \vec{D} =\]
Options
- \[2 \overrightarrow{OG}\]
- \[4 \overrightarrow{OG}\]
- \[5 \overrightarrow{OG}\]
- \[3 \overrightarrow{OG}\]
Solution
Let us consider the point O as origin.
G is the mid point of AC.
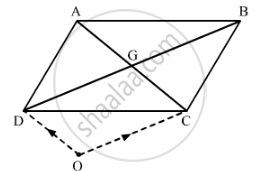
\[\therefore \overrightarrow{OG} = \frac{\overrightarrow{OA} + \overrightarrow{OC}}{2}\]
\[2 \overrightarrow{OG} = \overrightarrow{OA} + \overrightarrow{OC} . . . . . \left( 1 \right)\]
Also, G is the mid point BD
\[\therefore \overrightarrow{OG} = \frac{\overrightarrow{OB} + \overrightarrow{OD}}{2}\]
\[2 \overrightarrow{OG} = \overrightarrow{OB} + \overrightarrow{OD} . . . . . \left( 2 \right)\]
On adding (1) and (2) we get,
\[2 \overrightarrow{OG} + 2 \overrightarrow{OG} = \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} \]
\[4 \overrightarrow{OG} = \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} \]
\[ \therefore \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} = 4 \overrightarrow{OG}\]
APPEARS IN
RELATED QUESTIONS
If a vector makes angles α, β, γ with OX, OY and OZ respectively, then write the value of sin2 α + sin2 β + sin2 γ.
If \[\left| \overrightarrow{a} \right| = 4\] and \[- 3 \leq \lambda \leq 2\], then write the range of \[\left| \lambda \vec{a} \right|\].
Forces 3 O \[\vec{A}\], 5 O \[\vec{B}\] act along OA and OB. If their resultant passes through C on AB, then
If \[\vec{a} , \vec{b} , \vec{c}\] are three non-zero vectors, no two of which are collinear and the vector \[\vec{a} + \vec{b}\] is collinear with \[\vec{c} , \vec{b} + \vec{c}\] is collinear with \[\vec{a} ,\] then \[\vec{a} + \vec{b} + \vec{c} =\]
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] and \[\vec{d}\] are the position vectors of points A, B, C, D such that no three of them are collinear and \[\vec{a} + \vec{c} = \vec{b} + \vec{d} ,\] then ABCD is a
If OACB is a parallelogram with \[\overrightarrow{OC} = \vec{a}\text{ and }\overrightarrow{AB} = \vec{b} ,\] then \[\overrightarrow{OA} =\]
Find the vector equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0. Hence find whether the plane thus obtained contains the line \[\frac{x + 2}{5} = \frac{y - 3}{4} = \frac{z}{5}\] or not.
Find the components along the coordinate axes of the position vector of the following point :
R(–11, –9)
If` vec"a" = 2hat"i" + 3hat"j" + + hat"k", vec"b" = hat"i" - 2hat"j" + hat"k" "and" vec"c" = -3hat"i" + hat"j" + 2hat"k", "find" [vec"a" vec"b" vec"c"]`
Express `- hat"i" - 3hat"j" + 4hat"k"` as the linear combination of the vectors `2hat"i" + hat"j" - 4hat"k", 2hat"i" - hat"j" + 3hat"k"` and `3hat"i" + hat"j" - 2hat"k"`
Select the correct option from the given alternatives:
If `bar"a", bar"b", bar"c"` are non-coplanar unit vectors such that `bar"a"xx (bar"b"xxbar"c") = (bar"b"+bar"c")/sqrt2`, then the angle between `bar"a" "and" bar"b"` is
In a parallelogram ABCD, diagonal vectors are `bar"AC" = 2hat"i" + 3hat"j" + 4hat"k" and bar"BD" = - 6hat"i" + 7hat"j" - 2hat"k"`, then find the adjacent side vectors `bar"AB" and bar"AD"`.
Find the unit vectors that are parallel to the tangent line to the parabola y = x2 at the point (2, 4).
If a parallelogram is constructed on the vectors `bar"a" = 3bar"p" - bar"q", bar"b" = bar"p" + 3bar"q" and |bar"p"| = |bar"q"| = 2` and angle between `bar"p" and bar"q"` is `pi/3,` and angle between lengths of the sides is `sqrt7 : sqrt13`.
Show that the vector area of a triangle ABC, the position vectors of whose vertices are `bar"a", bar"b" and bar"c"` is `1/2[bar"a" xx bar"b" + bar"b" xx bar"c" + bar"c" xx bar"a"]`.
Find a unit vector perpendicular to the plane containing the point (a, 0, 0), (0, b, 0) and (0, 0, c). What is the area of the triangle with these vertices?
Find the volume of the parallelopiped spanned by the diagonals of the three faces of a cube of side a that meet at one vertex of the cube.
The points A(- a, -b), B (0, 0), C(a, b) and D(a2 , ab) are ______.
If `overline"u"` and `overline"v"` are unit vectors and θ is the acute angle between them, then `2overline"u" xx 3overline"v"` is a unit vector for ______
a and b are non-collinear vectors. If c = (x - 2)a + b and d = (2x + 1)a - b are collinear vectors, then the value of x = ______.
Find the unit vector in the direction of the sum of the vectors `vec"a" = 2hat"i" - hat"j" + 2hat"k"` and `vec"b" = -hat"i" + hat"j" + 3hat"k"`.
If `vec"a" = 2hat"i" - hat"j" + hat"k", vec"b" = hat"i" + hat"j" - 2hat"k"` and `vec"c" = hat"i" + 3hat"j" - hat"k"`, find `lambda` such that `vec"a"` is perpendicular to `lambdavec"b" + vec"c"`.
The area of the parallelogram whose adjacent sides are `hat"i" + hat"k"` and `2hat"i" + hat"j" + hat"k"` is ______.
If `|vec"a"|` = 8, `|vec"b"|` = 3 and `|vec"a" xx vec"b"|` = 12, then value of `vec"a" * vec"b"` is ______.
If `vec"a", vec"b", vec"c"` determine the vertices of a triangle, show that `1/2[vec"b" xx vec"c" + vec"c" xx vec"a" + vec"a" xx vec"b"]` gives the vector area of the triangle. Hence deduce the condition that the three points `vec"a", vec"b", vec"c"` are collinear. Also find the unit vector normal to the plane of the triangle.
If `vec"a"` and `vec"b"` are adjacent sides of a rhombus, then `vec"a" * vec"b"` = 0
Classify the following measures as scalar and vector.
40 watt
In Figure, identify the following vector.

Collinear but not equal
Four vectors `veca, vecb, vecc` and `vecx` satisfy the relation `(veca.vecx)vecb = vecc + vecx` where `vecb * veca` ≠ 1. The value of `vecx` in terms of `veca, vecb` and `vecc` is equal to
Let the vectors `vec(a)` such `vec(b)` that `|veca|` = 3 and `|vecb| = sqrt(2)/3`, then `veca xx vecb` is a unit vector if the angle between `veca` and `vecb` is
Unit vector along `vec(PQ)`, where coordinates of P and Q respectively are (2, 1, – 1) and (4, 4, – 7), is ______.
In the triangle PQR, `bar(PQ) = 2bara` and `bar(QR)=2barb`. The mid-point of PR is M. Find following vectors in terms of `bar a and bar b `.
- `bar("PR")`
- `bar("PM")`
- `bar("QM")`
Check whether the vectors `2hati + 2hatj + 3hatk, - 3hati + 3hatj +2 hatk and 3hati + 4hatk` from a triangle or not.
Find the value of λ for which the points (6, – 1, 2), (8, – 7, λ) and (5, 2, 4) are collinear.
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk` and `3hati + 4hatk` form a triangle or not.
Evaluate the following.
`int x^3/(sqrt1 + x^4) `dx
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
Consider the following statements and choose the correct option:
Statement 1: If `veca` and `vecb` represents two adjacent sides of a parallelogram then the diagonals are represented by `veca + vecb` and `veca - vecb`.
Statement 2: If `veca` and `vecb` represents two diagonals of a parallelogram then the adjacent sides are represented by `2(veca + vecb)` and `2(veca - vecb)`.
Which of the following is correct?
