Advertisements
Advertisements
प्रश्न
The position vectors of the points A, B, C are \[2 \hat{i} + \hat{j} - \hat{k} , 3 \hat{i} - 2 \hat{j} + \hat{k}\text{ and }\hat{i} + 4 \hat{j} - 3 \hat{k}\] respectively.
These points
पर्याय
form an isosceles triangle
form a right triangle
are collinear
form a scalene triangle
उत्तर
form an isosceles triangle
Given: Position vectors of A, B, C and \[\hat{i} + 4 \hat{j} - 3 \hat{k}\].
Then,
\[\overrightarrow{AB} = \left( 3 \hat{i} - 2 \hat{j} + \hat{k} \right) - \left( 2 \hat{i} + \hat{j} - \hat{k} \right) = \hat{i} - 3 \hat{j} + 2 \hat{k} \]
\[ \overrightarrow{BC} = \left( \hat{i} + 4 \hat{j} - 3 \hat{k} \right) - \left( 3 \hat{i} - 2 \hat{j} + \hat{k} \right) = - 2 \hat{i} + 6 \hat{j} - 4 \hat{k} \]
\[ \overrightarrow{CA} = \left( 2 \hat{i} + \hat{j} - \hat{k} \right) - \left( \hat{i} + 4 \hat{j} - 3 \hat{k} \right) = \hat{i} - 3 \hat{j} + 2 \hat{k}\]
\[\text{ Now, }\overrightarrow{\left| AB \right|} = \sqrt{1^2 + \left( - 3 \right)^2 + 2^2} = \sqrt{1 + 9 + 4} = \sqrt{14}\]
\[ \left| \overrightarrow{CA} \right| = \sqrt{1^2 + \left( - 3 \right)^2 + 2^2} = \sqrt{1 + 9 + 4} = \sqrt{14}\]
\[\left| \overrightarrow{BC} \right| = \sqrt{\left( - 2 \right)^2 + 6^2 + \left( - 4^2 \right)} = \sqrt{4 + 36 + 16} = \sqrt{56}\]
\[ \therefore \left| AB \right| = \left| \overrightarrow{CA} \right|\]
Hence, the triangle is isosceles as two of its sides are equal.
APPEARS IN
संबंधित प्रश्न
If \[\vec{a}\] and \[\vec{b}\] are two non-collinear vectors such that \[x \vec{a} + y \vec{b} = \vec{0} ,\] then write the values of x and y.
If G denotes the centroid of ∆ABC, then write the value of \[\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} .\]
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] are the position vectors of the vertices of an equilateral triangle whose orthocentre is at the origin, then write the value of \[\vec{a} + \vec{b} + \vec{c} .\]
Write a unit vector in the direction of \[\overrightarrow{a} = 3 \hat{i} + 2 \hat{j} + 6 \hat{k} .\]
Find a unit vector in the direction of \[\overrightarrow{a} = 2 \hat{i} - 3 \hat{j} + 6 \hat{k}\].
For what value of 'a' the vectors \[2 \hat{i} - 3 \hat{j} + 4 \hat{k} \text{ and }a \hat{i} + 6 \hat{j} - 8 \hat{k}\] are collinear?
In a triangle OAC, if B is the mid-point of side AC and \[\overrightarrow{OA} = \overrightarrow{a} , \overrightarrow{OB} = \overrightarrow{b}\], then what is \[\overrightarrow{OC}\].
If O and O' are circumcentre and orthocentre of ∆ ABC, then \[\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC}\] equals
If OACB is a parallelogram with \[\overrightarrow{OC} = \vec{a}\text{ and }\overrightarrow{AB} = \vec{b} ,\] then \[\overrightarrow{OA} =\]
Find the components along the coordinate axes of the position vector of the following point :
Q(–5, 1)
Find the position vector of the mid-point of the vector joining the points
In the triangle PQR, `bar"PQ" = bar"2a", bar"QR" = bar"2b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`.
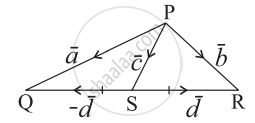
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Find a vector in the direction of `bara = hati - 2hatj` that has magnitude 7 units.
Find the coordinates of the point which is located three units behind the YZ-plane, four units to the right of XZ-plane, and five units above the XY-plane.
Select the correct option from the given alternatives:
If `bar"a" "and" bar"b"` are unit vectors, then what is the angle between `bar"a"` and `bar"b"` for `sqrt3bar"a" - bar"b"` to be a unit vector?
Let `bara = hati - hatj, barb = hatj - hatk, barc = hatk - hati.` If `bard` is a unit vector such that `bara * bard = 0 = [(barb, barc, bard)]`, then `bard` equals ______.
If ABC is a triangle whose orthocentre is P and the circumcentre is Q, prove that `bar"PA" + bar"PB" + bar"PC" = 2bar"PQ".`
If a parallelogram is constructed on the vectors `bar"a" = 3bar"p" - bar"q", bar"b" = bar"p" + 3bar"q" and |bar"p"| = |bar"q"| = 2` and angle between `bar"p" and bar"q"` is `pi/3,` and angle between lengths of the sides is `sqrt7 : sqrt13`.
Find the angle between the lines whose direction cosines are given by the equations 6mn - 2nl + 5lm = 0, 3l + m + 5n = 0.
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a".(bar"b".bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`(bar"a".bar"b")bar"c"`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`|bar"a"|(bar"b".bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a". bar"b" + bar"c"`
lf `overlinea` and `overlineb` be two unit vectors and θ is the angle between them, then `|overlinea - overlineb|` is equal to ______
For 0 < θ < π, if A = `[(costheta, -sintheta), (sintheta, costheta)]`, then ______
If `vec"a" = 2hat"i" - hat"j" + hat"k", vec"b" = hat"i" + hat"j" - 2hat"k"` and `vec"c" = hat"i" + 3hat"j" - hat"k"`, find `lambda` such that `vec"a"` is perpendicular to `lambdavec"b" + vec"c"`.
Using vectors, find the value of k such that the points (k, – 10, 3), (1, –1, 3) and (3, 5, 3) are collinear.
Classify the following as scalar and vector quantity.
Work done
In Figure, identify the following vector.

Collinear but not equal
If `veca ≠ vec(0), veca.vecb = veca.vecc, veca xx vecb = veca xx vecc`, then show that `vecb = vecc`.
Let `veca, vecb` and `vecc` be three unit vectors such that `veca xx (vecb xx vecc) = sqrt(3)/2 (vecb + vecc)`. If `vecb` is not parallel to `vecc`, then the angle between `veca` and `vecc` is
Which of the following measures as vector?
If two or more vectors are parallel to the same line, such vectors are known as:
Evaluate the following.
`int x^3/(sqrt1 + x^4) `dx
Check whether the vectors `2 hati+2 hatj+3 hatk,-3 hati+3 hatj+2 hatk and 3 hati +4 hatk` form a triangle or not.
