Advertisements
Advertisements
प्रश्न
If `veca ≠ vec(0), veca.vecb = veca.vecc, veca xx vecb = veca xx vecc`, then show that `vecb = vecc`.
उत्तर
We have `veca. (vecb - vecc)` = 0
⇒ `(vecb - vecc) = vec(0)` or `veca ⊥ (vecb - vecc)`
⇒ `vecb = vecc` or `veca ⊥ (vecb - vecc)`
Also `veca xx (vecb - vecc) = vec(0)`
⇒ `(vecb - vecc) = vec(0)` or `veca || (vecb - vecc)`
⇒ `vecb = vecc` or `veca || (vecb - vecc)`
`veca` cannot be both perpendicular to `(vecb - vecc)` and parallel to `(vecb - vecc)`
Hence, `vecb = vecc`.
APPEARS IN
संबंधित प्रश्न
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] represent the sides of a triangle taken in order, then write the value of \[\vec{a} + \vec{b} + \vec{c} .\]
If G denotes the centroid of ∆ABC, then write the value of \[\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} .\]
If D, E, F are the mid-points of the sides BC, CA and AB respectively of a triangle ABC, write the value of \[\overrightarrow{AD} + \overrightarrow{BE} + \overrightarrow{CF} .\]
Write a unit vector in the direction of \[\overrightarrow{a} = 3 \hat{i} + 2 \hat{j} + 6 \hat{k} .\]
If \[\overrightarrow{a} = \hat{i} + 2 \hat{j} - 3 \hat{k} \text{ and }\overrightarrow{b} = 2 \hat{i} + 4 \hat{j} + 9 \hat{k} ,\] find a unit vector parallel to \[\overrightarrow{a} + \overrightarrow{b}\].
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] and \[\vec{d}\] are the position vectors of points A, B, C, D such that no three of them are collinear and \[\vec{a} + \vec{c} = \vec{b} + \vec{d} ,\] then ABCD is a
The position vectors of the points A, B, C are \[2 \hat{i} + \hat{j} - \hat{k} , 3 \hat{i} - 2 \hat{j} + \hat{k}\text{ and }\hat{i} + 4 \hat{j} - 3 \hat{k}\] respectively.
These points
Find the vector equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0. Hence find whether the plane thus obtained contains the line \[\frac{x + 2}{5} = \frac{y - 3}{4} = \frac{z}{5}\] or not.
Find the value of λ for which the four points with position vectors `6hat"i" - 7hat"j", 16hat"i" - 19hat"j" - 4hat"k" , lambdahat"j" - 6hat"k" "and" 2hat"i" - 5hat"j" + 10hat"k"` are coplanar.
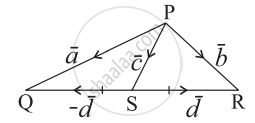
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Find the distance from (4, - 2, 6) to each of the following:
(a) The XY-plane
(b) The YZ-plane
(c) The XZ-plane
(d) The X-axis
(e) The Y-axis
(f) The Z-axis.
Select the correct option from the given alternatives:
Let a, b, c be distinct non-negative numbers. If the vectors `"a"hat"i" + "a"hat"j" + "c"hat"k" , hat"i" + hat"k" "and" "c"hat"i" + "c"hat"j" + "b"hat"k"` lie in a plane, then c is
Two sides of a parallelogram are `3hat"i" + 4hat"j" - 5hat"k"` and `-2hat"j" + 7hat"k"`. Find the unit vectors parallel to the diagonals.
ABCD is a parallelogram. E, F are the midpoints of BC and CD respectively. AE, AF meet the diagonal BD at Q and P respectively. Show that P and Q trisect DB.
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a". bar"b" + bar"c"`
If `bar"a", bar"b", bar"c"` are three non-coplanar vectors show that `(bar"a".(bar"b" xx bar"c"))/((bar"c" xx bar"a").bar"b") + (bar"b".(bar"a" xx bar"c"))/((bar"c" xx bar"a").bar"b") = 0`
For any non-zero vectors a and b, [b a × b a] = ?
If the points (–1, –1, 2), (2, m, 5) and (3,11, 6) are collinear, find the value of m.
The area of the parallelogram whose adjacent sides are `hat"i" + hat"k"` and `2hat"i" + hat"j" + hat"k"` is ______.
The unit vector perpendicular to the vectors `hat"i" - hat"j"` and `hat"i" + hat"j"` forming a right handed system is ______.
If `vec"a"` is any non-zero vector, then `(vec"a" .hat"i")hat"i" + (vec"a".hat"j")hat"j" + (vec"a".hat"k")hat"k"` equals ______.
Classify the following measures as scalar and vector.
40 watt
Classify the following measures as scalar and vector.
20 m/s2
If `veca` and `vecb` are two collinear vectors then which of the following are incorrect.
If `veca = hati - hatj + 7hatk` and `vecb = 5hati - hatj + λhatk`, then find the value of λ so that the vectors `veca + vecb` and `veca - vecb` are orthogonal.
In the triangle PQR, `bar"PQ" = 2 bar" a" and bar"QR" = 2 bar"b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
Check whether the vectors `2hati+2hatj+3hatk,-3hati+3hatj+2hatk` and `3hati+4hatk` form a triangle or not.
In the triangle PQR, `bar(PQ)`= 2`bar a` and `bar(QR)`= 2`bar b` . The mid-point of PR is M. Find following vectors in terms of `bara` and `barb`.
- `bar(PR)`
- `bar(PM)`
- `bar(QM)`
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
