Advertisements
Advertisements
प्रश्न
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a". bar"b" + bar"c"`
उत्तर
This is the sum of scalar and vector which is not defined. Therefore, this expression is meaningless.
APPEARS IN
संबंधित प्रश्न
Write the position vector of a point dividing the line segment joining points A and B with position vectors \[\vec{a}\] and \[\vec{b}\] externally in the ratio 1 : 4, where \[\overrightarrow{a} = 2 \hat{i} + 3 \hat{j} + 4 \hat{k} \text{ and }\overrightarrow{b} = - \hat{i} + \hat{j} + \hat{k} .\]
Write the position vector of a point dividing the line segment joining points having position vectors \[\hat{i} + \hat{j} - 2 \hat{k} \text{ and }2 \hat{i} - \hat{j} + 3 \hat{k}\] externally in the ratio 2:3.
If points A (60 \[\hat{i}\] + 3 \[\hat{j}\]), B (40 \[\hat{i}\] − 8 \[\hat{j}\]) and C (a \[\hat{i}\] − 52 \[\hat{j}\]) are collinear, then a is equal to
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] and \[\vec{d}\] are the position vectors of points A, B, C, D such that no three of them are collinear and \[\vec{a} + \vec{c} = \vec{b} + \vec{d} ,\] then ABCD is a
The position vectors of the points A, B, C are \[2 \hat{i} + \hat{j} - \hat{k} , 3 \hat{i} - 2 \hat{j} + \hat{k}\text{ and }\hat{i} + 4 \hat{j} - 3 \hat{k}\] respectively.
These points
Find the components along the coordinate axes of the position vector of the following point :
Q(–5, 1)
In Figure, which of the following is not true?
Find the value of λ for which the four points with position vectors `6hat"i" - 7hat"j", 16hat"i" - 19hat"j" - 4hat"k" , lambdahat"j" - 6hat"k" "and" 2hat"i" - 5hat"j" + 10hat"k"` are coplanar.
Find a unit vector perpendicular to each of the vectors `veca + vecb "and" veca - vecb "where" veca = 3hati + 2hatj + 2hatk and vecb = i + 2hatj - 2hatk`
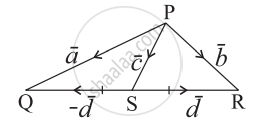
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Find the coordinates of the point which is located in the YZ-plane, one unit to the right of the XZ- plane, and six units above the XY-plane.
If the sum of two unit vectors is itself a unit vector, then the magnitude of their difference is ______.
Select the correct option from the given alternatives:
If `|bar"a"| = 3` and - 1 ≤ k ≤ 2, then `|"k"bar"a"|` lies in the interval
Select the correct option from the given alternatives:
Let a, b, c be distinct non-negative numbers. If the vectors `"a"hat"i" + "a"hat"j" + "c"hat"k" , hat"i" + hat"k" "and" "c"hat"i" + "c"hat"j" + "b"hat"k"` lie in a plane, then c is
Select the correct option from the given alternatives:
If `bar"a", bar"b", bar"c"` are non-coplanar unit vectors such that `bar"a"xx (bar"b"xxbar"c") = (bar"b"+bar"c")/sqrt2`, then the angle between `bar"a" "and" bar"b"` is
Find the unit vectors that are parallel to the tangent line to the parabola y = x2 at the point (2, 4).
The XZ plane divides the line segment joining the points (3, 2, b) and (a, -4, 3) in the ratio ______.
The vector eqliation of line 2x - 2 = 3y + 1 = 6z - 2 is
The points A(- a, -b), B (0, 0), C(a, b) and D(a2 , ab) are ______.
a and b are non-collinear vectors. If p = (2x + 1) a - band q = (x - 2)a +b are collinear vectors, then x = ______.
a and b are non-collinear vectors. If c = (x - 2)a + b and d = (2x + 1)a - b are collinear vectors, then the value of x = ______.
For any non zero vector, a, b, c a · ((b + c) × (a + b + c)] = ______.
The angle between the vectors `hat"i" - hat"j"` and `hat"j" - hat"k"` is ______.
If `vec"a" = hat"i" + hat"j" + 2hat"k"` and `vec"b" = 2hat"i" + hat"j" - 2hat"k"`, find the unit vector in the direction of `6vec"b"`
Find a unit vector in the direction of `vec"PQ"`, where P and Q have co-ordinates (5, 0, 8) and (3, 3, 2), respectively
Classify the following measures as scalar and vector.
20 m/s2
Classify the following as scalar and vector quantity.
Distance
Classify the following as scalar and vector quantity.
Velocity
Classify the following as scalar and vector quantity.
Work done
`bara, barb` and `barc` are three vectors such that `veca + vecb + vecc` 20, `|bara| = 1, |barb| = 2` and `|barc| = 3`. Then `bara. barb + barb.barc + bar(c.a)` is equal to
Find `|veca xx vecb|`, if `veca = hati - 7hatj + 7hatk` and `vecb = 3hati - 2hatj + 2hatk`
If `veca = hati - hatj + 7hatk` and `vecb = 5hati - hatj + λhatk`, then find the value of λ so that the vectors `veca + vecb` and `veca - vecb` are orthogonal.
The angles of a triangle, two of whose sides are represented by the vectors `sqrt(3)(veca xx vecb)` and `vecb - (veca.vecb)veca` where `vecb` is a non-zero vector and `veca` is a unit vector are ______.
Check whether the vectors `2hati + 2hatj + 3hatk, - 3hati + 3hatj +2 hatk and 3hati + 4hatk` from a triangle or not.
If `hata` is unit vector and `(2vecx - 3hata)*(2vecx + 3hata)` = 91, find the value of `|vecx|`.
In the triangle PQR, `bar(PQ)=2bara` and `bar(QR)=2barb`. The mid-point of PR is M. Find following vectors in terms of `bara and barb`.
(i) `bar(PR)` (ii) `bar(PM)` (iii) `bar(QM)`
Check whether the vectors `2 hati+2 hatj+3 hatk,-3 hati+3 hatj+2 hatk and 3 hati +4 hatk` form a triangle or not.
Check whether the vectors `2hati + 2hatj +3hatk, - 3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
In the triangle PQR, `bar(PQ)` = 2`bara` and `bar(QR)` = 2`barb`. The midpoint of PR is M. Find the following vectors in terms of `bara` and `barb`.
(i) `bar(PR)` (ii) `bar(PM)` (iii) `bar(QM)`
