Advertisements
Advertisements
प्रश्न
Find the number of sides in a regular polygon, if its interior angle is equal to its exterior angle.
उत्तर
Let each exterior angle or interior angle be = x°
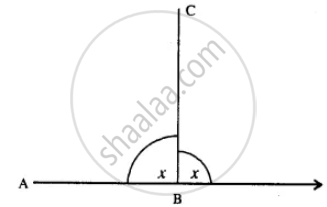
∴ x + x = 180°
2x = 180°
x = 90°
Now, let no. of sides = n
∵ each exterior angle = `360^circ/"n"`
∴ 90° = `360^circ/"n"`
n = `360^circ/90^circ`
n = 4
APPEARS IN
संबंधित प्रश्न
Find the number of sides in a regular polygon, if its interior angle is: 160°
Find the number of sides in a regular polygon, if its interior angle is: `1 1/5` of a right angle
Find the number of sides in a regular polygon, if its exterior angle is: two-fifth of right angle
Is it possible to have a regular polygon whose interior angle is : 170°
The exterior angle of a regular polygon is one-third of its interior angle. Find the number of sides in the polygon.
The measure of each interior angle of a regular polygon is five times the measure of its exterior angle. Find :
(i) measure of each interior angle ;
(ii) measure of each exterior angle and
(iii) number of sides in the polygon.
The ratio between the exterior angle and the interior angle of a regular polygon is 1 : 4. Find the number of sides in the polygon.
Two alternate sides of a regular polygon, when produced, meet at the right angle. Calculate the number of sides in the polygon.
In a regular pentagon ABCDE, draw a diagonal BE and then find the measure of:
(i) ∠BAE
(ii) ∠ABE
(iii) ∠BED
Calculate the number of sides of a regular polygon, if: its interior angle is five times its exterior angle.
