Advertisements
Advertisements
प्रश्न
Find the slope of a line having inclination 60°.
उत्तर
slope = tan θ
= tan 60° = `sqrt(3)`
APPEARS IN
संबंधित प्रश्न
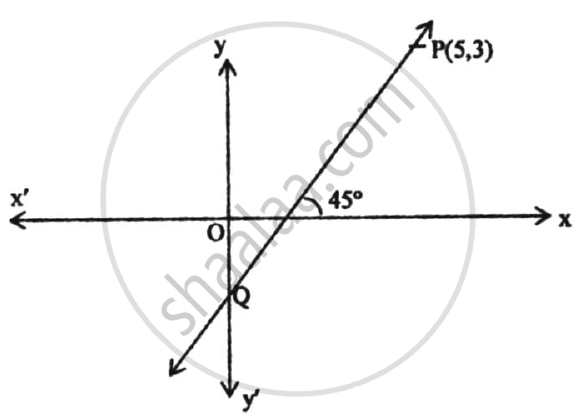
The line through P(5, 3) intersects y-axis at Q.
(1) Write the slope of the line.
(2) Write the equation of the line.
(3) Find the coordinates of Q.
Find the slope of the line parallel to AB if : A = (−2, 4) and B = (0, 6)
Find the slope of the line perpendicular to AB if : A = (3, −2) and B = (−1, 2)
The side AB of an equilateral triangle ABC is parallel to the x-axis. Find the slopes of all its sides.

Find the slope and the inclination of the line AB if : A = `(0, - sqrt(3))` and B = (3, 0)
Find the slope of the line which is perpendicular to `x - y/2 + 3 = 0`
The line through A(−2, 3) and B(4, b) is perpendicular to the line 2x – 4y = 5. Find the value of b.
The ordinate of a point lying on the line joining the points (6, 4) and (7, –5) is –23. Find the coordinates of that point.
Angle made by the line with the positive direction of X-axis is given. Find the slope of the line.
45°
Fill in the blank using correct alternative.
Distance of point (–3, 4) from the origin is ______.
Determine whether the given point is collinear.
A (0, 2), B (1, -0.5), C (2, -3)
Find k if the line passing through points P(–12, –3) and Q(4, k) has slope \[\frac{1}{2}\].
Find the slope of a line, correct of two decimals, whose inclination is 60°
Find the slope of a line passing through the given pair of points (3,7) and (5,13)
Find the slope and the y-intercept of the following line 2x + 3y = 12
Find slope of a line passing through the points A(3, 1) and B(5, 3).
Write the equation of a line passing through the point P (0,6) and having slope 6/7.
Show that points A(– 4, –7), B(–1, 2), C(8, 5) and D(5, – 4) are the vertices of a parallelogram ABCD
Determine whether the following points are collinear. A(–1, –1), B(0, 1), C(1, 3)
Given: Points A(–1, –1), B(0, 1) and C(1, 3)
Slope of line AB = `(square - square)/(square - square) = square/square` = 2
Slope of line BC = `(square - square)/(square - square) = square/square` = 2
Slope of line AB = Slope of line BC and B is the common point.
∴ Points A, B and C are collinear.
