Advertisements
Advertisements
प्रश्न
Find the vector and Cartesian equation of the planes that passes through the point (1, 0, −2) and the normal to the plane is `hati + hatj - hatk`
उत्तर
The position vector of point (1, 0, −2) is `veca = hati - 2hatk`
The normal vector `vecN` perpendicular to the plane is `vecN = hati + hatj - hatk`
The vector equation of the plane is given by, `(vecr-veca).vecN = 0`
`=>[vecrr - (hati -2hatk)].(hati + hatj - hatk) = 0`
`vecr `is the position vector of any point P (x, y, z) in the plane.
`:. vecr = xhati + yhatj + zhatk`
Therefore, equation (1) becomes
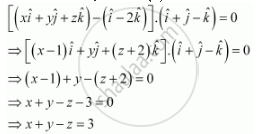
This is the Cartesian equation of the required plane.
APPEARS IN
संबंधित प्रश्न
Find the vector equation of the plane passing through a point having position vector `3 hat i- 2 hat j + hat k` and perpendicular to the vector `4 hat i + 3 hat j + 2 hat k`
Parametric form of the equation of the plane is `bar r=(2hati+hatk)+lambdahati+mu(hat i+2hatj+hatk)` λ and μ are parameters. Find normal to the plane and hence equation of the plane in normal form. Write its Cartesian form.
Write the vector equation of the plane, passing through the point (a, b, c) and parallel to the plane `vec r.(hati+hatj+hatk)=2`
Find the vector equation of the plane which contains the line of intersection of the planes `vecr (hati+2hatj+3hatk)-4=0` and `vec r (2hati+hatj-hatk)+5=0` which is perpendicular to the plane.`vecr(5hati+3hatj-6hatk)+8=0`
Find the vector equation of the plane with intercepts 3, –4 and 2 on x, y and z-axis respectively.
Find the equation of the plane which contains the line of intersection of the planes
`vecr.(hati-2hatj+3hatk)-4=0" and"`
`vecr.(-2hati+hatj+hatk)+5=0`
and whose intercept on x-axis is equal to that of on y-axis.
Find the vector equation of a plane which is at a distance of 5 units from the origin and its normal vector is `2hati-3hatj+6hatk`
Find the vector equation of a line passing through the points A(3, 4, –7) and B(6, –1, 1).
Find the Cartesian equation of the following planes:
`vecr.(2hati + 3hatj-4hatk) = 1`
Find the Cartesian equation of the following planes:
`vecr.[(s-2t)hati + (3 - t)hatj + (2s + t)hatk] = 15`
In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin.
2x + 3y + 4z – 12 = 0
In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin.
3y + 4z – 6 = 0
Find the vector and Cartesian equation of the planes that passes through the point (1, 4, 6) and the normal vector to the plane is `hati -2hatj + hatk`
Find the cartesian form of the equation of the plane `bar r=(hati+hatj)+s(hati-hatj+2hatk)+t(hati+2hatj+hatj)`
Find the equation of the plane through the line of intersection of `vecr*(2hati-3hatj + 4hatk) = 1`and `vecr*(veci - hatj) + 4 =0`and perpendicular to the plane `vecr*(2hati - hatj + hatk) + 8 = 0`. Hence find whether the plane thus obtained contains the line x − 1 = 2y − 4 = 3z − 12.
The Cartesian equation of the line is 2x - 3 = 3y + 1 = 5 - 6z. Find the vector equation of a line passing through (7, –5, 0) and parallel to the given line.
Find the image of a point having the position vector: `3hati - 2hatj + hat k` in the plane `vec r.(3hati - hat j + 4hatk) = 2`
Find the vector and Cartesian forms of the equation of the plane passing through the point (1, 2, −4) and parallel to the lines \[\vec{r} = \left( \hat{i} + 2 \hat{j} - 4 \hat{k} \right) + \lambda\left( 2 \hat{i} + 3 \hat{j} + 6 \hat{k} \right)\] and \[\vec{r} = \left( \hat{i} - 3 \hat{j} + 5 \hat{k} \right) + \mu\left( \hat{i} + \hat{j} - \hat{k} \right)\] Also, find the distance of the point (9, −8, −10) from the plane thus obtained.
Find the vector equation of the line passing through (1, 2, 3) and parallel to the planes \[\vec{r} \cdot \left( \hat{i} - \hat{j} + 2 \hat{k} \right) = 5 \text{ and } \vec{r} \cdot \left( 3 \hat{i} + \hat{j} + \hat{k} \right) = 6 .\]
Find the vector and cartesian equations of the plane passing throuh the points (2,5,- 3), (-2, - 3,5) and (5,3,-3). Also, find the point of intersection of this plane with the line passing through points (3, 1, 5) and (–1, –3, –1).
Find the Cartesian equation of the plane, passing through the line of intersection of the planes `vecr. (2hati + 3hatj - 4hatk) + 5 = 0`and `vecr. (hati - 5hatj + 7hatk) + 2 = 0` intersecting the y-axis at (0, 3).
Find the vector and cartesian equation of the plane passing through the point (2, 5, - 3), (-2, -3, 5) and (5, 3, -3). Also, find the point of intersection of this plane with the line passing through points (3, 1, 5) and (-1, -3, -1).
Find the vector and Cartesian equations of the plane passing through the points (2, 2 –1), (3, 4, 2) and (7, 0, 6). Also find the vector equation of a plane passing through (4, 3, 1) and parallel to the plane obtained above.
Find the vector equation of the plane that contains the lines `vecr = (hat"i" + hat"j") + λ (hat"i" + 2hat"j" - hat"k")` and the point (–1, 3, –4). Also, find the length of the perpendicular drawn from the point (2, 1, 4) to the plane thus obtained.
The vector equation of the line `(x - 5)/3 = (y + 4)/7 = (z - 6)/2` is ______.
The vector equation of the line `(x - 5)/3 = (y + 4)/7 = (z - 6)/2` is `vec"r" = 5hat"i" - 4hat"j" + 6hat"k" + lambda(3hat"i" + 7hat"j" + 2hat"k")`.
