Advertisements
Advertisements
प्रश्न
Find the zeroes of the quadratic polynomial `f(x) = 6x^2 – 3.`
उत्तर
To find the zeroes of the quadratic polynomial we will equate f(x) to 0
`∴f(x) = 0`
`⇒ 6x^2 – 3 = 0`
`⇒ 3(2x^2 – 1) = 0`
`⇒ 2x^2 – 1 = 0`
`⇒2x^2 = 1 `
`⇒x^2=1/2`
`⇒ x=+-1/sqrt2`
Hence, the zeroes of the quadratic polynomial f(x) = `6x^2-3 are 1/sqrt2,-1/sqrt2`
APPEARS IN
संबंधित प्रश्न
Find the zeros of the polynomial `f(x) = x^2 + 7x + 12` and verify the relation between its zeroes and coefficients.
Find all the zeroes of polynomial `(2x^4 – 11x^3 + 7x^2 + 13x – 7)`, it being given that two of its zeroes are `(3 + sqrt2) and (3 – sqrt2)`.
If 𝛼, 𝛽 are the zeroes of the polynomial `f(x) = x^2 – 5x + k` such that 𝛼 - 𝛽 = 1, find the value of k = ?
A quadratic polynomial, whose zeores are -4 and -5, is ______.
If x4 + 3x2 + 7 is divided by 3x + 5, then the possible degrees of quotient and remainder are ______.
If one of the zeroes of the cubic polynomial x3 + px² + qx + r is -1, then the product of the other two zeroes is ______.
If 4x² – 6x – m is divisible by x – 3, the value of m is exact divisor of ______.
If the graph of a polynomial intersects the x-axis at only one point, it cannot be a quadratic polynomial.
If the graph of a polynomial intersects the x-axis at exactly two points, it need not be a quadratic polynomial.
The graph of y = f(x) is shown in the figure for some polynomial f(x).
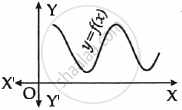
The number of zeroes of f(x) is ______.
