Advertisements
Advertisements
प्रश्न
For the sectors with given measures, find the length of the arc, area and perimeter. (π = 3.14)
central angle 120°, d = 12.6 cm
उत्तर
∴ r = `12.6/2 "cm"`
r = 6.3 cm
Length of the arc l = `(theta^circ)/(360^circ) xx 2pi"r" "units"`
l = `(120^circ)/(360^circ) xx 2 xx 3.14 xx 63 "cm"`
l = 13.188 cm
I = 13.19 cm
Area of the sector A = `(theta^circ)/(360^circ) xx pi"r"^2 "units"`
A = `(120^circ)/(360^circ) xx 3.14 xx 6.3 xx 63 "cm"^2`
A = 3.14 × 6.3 × 2.1 cm2
A = 41.54 cm2
Perimeter of the sector P = l + 2r cm
P = 13.19 + 2(6.3) cm
= 13.19 + 12.6 cm
P = 25.79 cm
APPEARS IN
संबंधित प्रश्न
The radius of a circle is 10 cm. The measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (\[\pi\]= 3.14 )
The measure of an arc of a circle is 80° and its radius is 18 cm. Find the length of the arc. (π = 3.14)
The area of a sector of a circle of 6 cm radius is 15 \[\pi\] sq.cm. Find the measure of the arc and length of the arc corresponding to the sector.
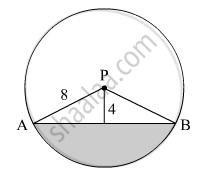
In the given figure, seg AB is a chord of a circle with centre P. If PA = 8 cm and distance of chord AB from the centre P is 4 cm, find the area of the shaded portion. ( \[\pi\] = 3.14, \[\sqrt{3}\]= 1.73 )
In Δ ABC, if ∠ A = 65° ; ∠ B = 40° then find the measure of ∠ C.
Measure of an arc of a sector of a circle is 900 and its radius is 7cm. Find the perimeter of the sector.
(A) 44 cm (B) 25 cm (C) 36 cm (D) 56 cm
For the sectors with given measures, find the length of the arc, area and perimeter. (π = 3.14)
central angle 45°, r = 16 cm
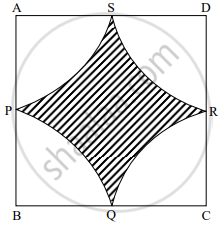
In the given figure `square`ABCD is a square of side 50 m. Points P, Q, R, S are midpoints of side AB, side BC, side CD, side AD respectively. Find area of shaded region
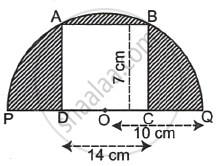
In the given figure, a rectangle ABCD is inscribed inside a semi-circle of radius 10 cm. Using the dimensions given in the figure, determine the area of the shaded region.
The perimeter of an arc of radius 4.2 cm is 12.8 cm. Determine the angle subtended by the arc at the centre of circle.
