Advertisements
Advertisements
प्रश्न
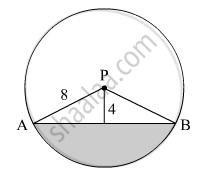
In the given figure, seg AB is a chord of a circle with centre P. If PA = 8 cm and distance of chord AB from the centre P is 4 cm, find the area of the shaded portion. ( \[\pi\] = 3.14, \[\sqrt{3}\]= 1.73 )
उत्तर
Draw PQ ⊥ AB.
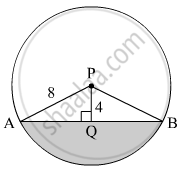
∴ AQ = QB (Perpendicular from the centre of the circle to the chord bisects the chord)
In right ∆APQ,
\[AQ = \sqrt{{AP}^2 - {PQ}^2}\]
\[ \Rightarrow AQ = \sqrt{8^2 - 4^2}\]
\[ \Rightarrow AQ = \sqrt{64 - 16}\]
\[ \Rightarrow AQ = \sqrt{48}\]
\[ \Rightarrow AQ = 4\sqrt{3}\text{ cm} \]
∴ AB = 2AQ = \[2 \times 4\sqrt{3} = 8\sqrt{3} \text{ cm }\]
Also,
\[ \Rightarrow \sin\angle APQ = \frac{4\sqrt{3}}{8}\]
\[ \Rightarrow \sin\angle APQ = \frac{\sqrt{3}}{2} = \sin60°\]
\[ \Rightarrow \angle APQ = 60°\]
Radius of the circle, r = 8 cm
Measure of arc AB, θ = 120º
∴ Area of the shaded portion = Area of the sector ABP − Area of ∆APB
\[ = \frac{120° }{360° } \times 3 . 14 \times 8^2 - \frac{1}{2} \times 8\sqrt{3} \times 4\]
\[ = 66 . 97 - 27 . 68\]
\[ = 39 . 29 {cm}^2\]
Thus, the area of the shaded portion is 39.29 cm2.
संबंधित प्रश्न
The radius of a circle is 10 cm. The measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (\[\pi\]= 3.14 )
The measure of an arc of a circle is 80° and its radius is 18 cm. Find the length of the arc. (π = 3.14)
The area of a sector of a circle of 6 cm radius is 15 \[\pi\] sq.cm. Find the measure of the arc and length of the arc corresponding to the sector.
Length of a rectangular tank is twice its breadth. If the
depth of the tank is 3 m and area of its four walls is 108 m2, find the
length of the tank.
Find the length of an arc if measure of the arc is 90° and its radius
is 14 cm.
Measure of an arc of a sector of a circle is 900 and its radius is 7cm. Find the perimeter of the sector.
(A) 44 cm (B) 25 cm (C) 36 cm (D) 56 cm
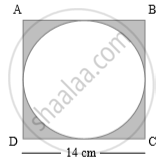
A circle is inscribed in square ABCD of side 14 cm. Complete the following activity to find the area of the shaded portion.
Activity:
Area of square ABCD = ______
= 142
= 196 cm2
Area of circle = πr2 = `22/7xx 7^2`
= ____ cm2
Area of shaded portion = Area of square ABCD – Area of circle
= 196 – _______
= _____ cm2
For the sectors with given measures, find the length of the arc, area and perimeter. (π = 3.14)
central angle 45°, r = 16 cm
For the sectors with given measures, find the length of the arc, area and perimeter. (π = 3.14)
central angle 120°, d = 12.6 cm
A circle of radius 120 m is divided into 8 equal sectors. Find the length of the arc of each of the sectors
Two gates are fitted at the entrance of a library. To open the gates easily, a wheel is fixed at 6 feet distance from the wall to which the gate is fixed. If one of the gates is opened to 90°, find the distance moved by the wheel (π = 3.14)
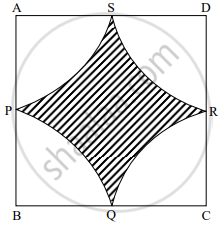
In the given figure `square`ABCD is a square of side 50 m. Points P, Q, R, S are midpoints of side AB, side BC, side CD, side AD respectively. Find area of shaded region
The perimeter of an arc of radius 4.2 cm is 12.8 cm. Determine the angle subtended by the arc at the centre of circle.
