Advertisements
Advertisements
प्रश्न
Given below are densities of some solids and liquids. Give rough estimates of the size of their atoms:
| Substance | Atomic Mass (u) | Density (103 Kg m-3) |
| Carbon (diamond) | 12.01 | 2.22 |
| Gold | 197.00 | 19.32 |
| Nitrogen (liquid) | 14.01 | 1.00 |
| Lithium | 6.94 | 0.53 |
| Fluorine (liquid) | 19.00 | 1.14 |
[Hint: Assume the atoms to be ‘tightly packed’ in a solid or liquid phase, and use the known value of Avogadro’s number. You should, however, not take the actual numbers you obtain for various atomic sizes too literally. Because of the crudeness of the tight packing approximation, the results only indicate that atomic sizes are in the range of a few Å].
उत्तर १
| Substance | Radius (Å) |
| Carbon (diamond) | 1.29 |
| Gold | 1.59 |
| Nitrogen (liquid) | 1.77 |
| Lithium | 1.73 |
| Fluorine (liquid) | 1.88 |
Atomic mass of a substance = M
Density of the substance = ρ
Avogadro’s number = N = 6.023 × 1023
Volume of each atom = `4/3 pi r^3`
Volume of N number of molecules = `4/3 pir^3N` ... (i)
Volume of one mole of a substance = `M/rho` ... (ii)
`4/3 pir^3 N = M/rho`
`:. r = root(3)((3m)/(4pirhoN))`
For carbon
M = 12.01 × 10–3 kg,
ρ = 2.22 × 103 kg m–3
`:. r = ((3xx12.01xx10^(-3))/(4pixx2.22xx10^3xx6.023xx 10^23))^(1/3)` = 1.29 Å
For gold:
M = 197.00 × 10–3 kg
ρ = 19.32 × 103 kg m–3
:. r = `((3xx197xx10^3)/(4pixx19.32xx10^3xx6.023xx10^23))^(1/3)` = 1.59 Å
Hence, the radius of a gold atom is 1.59 Å.
For liquid nitrogen:
M = 14.01 × 10–3 kg
ρ = 1.00 × 103 kg m–3
`:. r = ((3xx14.01xx10^(-3))/(4pixx1.00xx10^3xx 6.23 xx10^23))^(1/3)` = 1.77 Å
Hence, the radius of a liquid nitrogen atom is 1.77 Å.
For lithium:
M = 6.94 × 10–3 kg
ρ = 0.53 × 103 kg m–3
`:. r= ((3xx6.94xx10^(-3))/(4pixx0.53xx10^3xx6.23xx10^23))^(1/3)` = 1.73 Å
Hence, the radius of a lithium atom is 1.73 Å.
For liquid fluorine:
M = 19.00 × 10–3 kg
ρ = 1.14 × 103 kg m–3
`:. r= ((3xx19xx10^(-3))/(4pixx1.14xx10^3xx6.023xx10^23))^(1/3)` = = 1.88 Å
Hence, the radius of a liquid fluorine atom is 1.88 Å.
उत्तर २
In one mole of a substance, there are 6.023 x 1023 atoms
`:. (4/3 pi R^3) xx 6.023 xx 10^23 = M/rho`
or ` R = [(3M)/(4pirho xx 6.023xx10^23)]^(1/3)`
For carbon = `12.01 xx 10^(-3)` kg and `rho = 2.22 xx 10^3 "kg m"^(-3)`
`:. R = [(3xx12.01xx10^(-3))/(4xx3.14xx2.22xx10^3xx6.023xx10^23)]^(1/3)`
= `1.29 xx 10^(10) m` = 1.29 Å
For gold, M = `197 xx10^(-3)` kg and `rho = 19.32 xx 10^3 "kg m"^(-3)`
`:. R = [(3xx197xx10^(-3))/(4xx3.14xx19.32xx10^3 xx 6.023 xx 10^(23))]^(1/3)`
= 1.59 xx 10^(-10) m = 1.59 Å
For nitrogen (liquid), `M= 14.01 xx 10^(-3)` kg and `rho = 1.00 xx 10^3 "kg m"^(-3)`
`R = [(3xx14.01xx10^(-3))/(4xx3.14xx100xx10^3xx6.023xx10^23)]^(1/3)`
= `1.77 xx 10^(-10)m` = 1.77 Å
For lithium, M= `6.94 xx 10^(-3)` kg, `rho = 0.53 xx 10^3 "kg m"^(-3)`
`:. R = [(3xx6.94xx10^(-3))/(4xx3.14xx0.53xx10^3xx6.023xx10^(23))]^(1/3)`
`= 1.73 xx 10^(-10)` = 1.73 Å
For fluorine (liquid), M = `19.00 xx 10^(-3)` kg, `rho = 1.14 xx 10^3 "kg m"^(-3)`
`:. R = [(3xx19.00xx10^(-3))/(4xx3.14xx1.14xx10^3xx6.023xx10^(23))]^(`1/3)`
`= 1.88 xx 10^(-10)m` = 1.88 Å
APPEARS IN
संबंधित प्रश्न
The specific heat capacity of water is
Does a solid also have two kinds of molar heat capacities Cp and Cv? If yes, is Cp > Cv? Or is Cp − Cv = R?
Two samples A and B are initially kept in the same state. Sample A is expanded through an adiabatic process and the sample B through an isothermal process. The final volumes of the samples are the same. The final pressures in A and B are pA and pBrespectively.
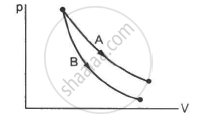
Consider the processes A and B shown in the figure. It is possible that
A sample of air weighing 1.18 g occupies 1.0 × 103 cm3 when kept at 300 K and 1.0 × 105 Pa. When 2.0 cal of heat is added to it at constant volume, its temperature increases by 1°C. Calculate the amount of heat needed to increase the temperature of air by 1°C at constant pressure if the mechanical equivalent of heat is 4.2 × 107 erg cal−1. Assume that air behaves as an ideal gas.
An ideal gas expands from 100 cm3 to 200 cm3 at a constant pressure of 2.0 × 105 Pa when 50 J of heat is supplied to it. Calculate (a) the change in internal energy of the gas (b) the number of moles in the gas if the initial temperature is 300 K (c) the molar heat capacity Cp at constant pressure and (d) the molar heat capacity Cv at constant volume.
A mixture contains 1 mole of helium (Cp = 2.5 R, Cv = 1.5 R) and 1 mole of hydrogen (Cp= 3.5 R, Cv = 2.5 R). Calculate the values of Cp, Cv and γ for the mixture.
4.0 g of helium occupies 22400 cm3 at STP. The specific heat capacity of helium at constant pressure is 5.0 cal K−1 mol−1. Calculate the speed of sound in helium at STP.
A diatomic molecule can be modelled as two rigid balls connected with spring such that the balls can vibrate with respect to centre of mass of the system (spring + balls). Consider a diatomic gas made of such diatomic molecule. If the gas performs 20 Joule of work under isobaric condition, then heat given to the gas is ______ J.
If at same temperature and pressure, the densities for two diatomic gases are respectively d1 and d2 then the ratio of velocities of sound in these gases will be ______.
