Advertisements
Advertisements
प्रश्न
Given figure depicts an archery target marked with its five scoring areas from the centre outwards as Gold, Red, Blue, Black and White. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions. [use π = 22/7]

उत्तर
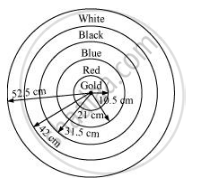
Radius (r1) of gold region (i.e., 1st circle) = 21/2 = 10.5 cm
Given that each circle is 10.5 cm wider than the previous circle.
Therefore, radius (r2) of 2nd circle = 10.5 + 10.5
21 cm
Radius (r3) of 3rd circle = 21 + 10.5
= 31.5 cm
Radius (r4) of 4th circle = 31.5 + 10.5
= 42 cm
Radius (r5) of 5th circle = 42 + 10.5
= 52.5 cm
Area of gold region = Area of 1st circle = `pir_1^2 = pi(10.5)^2 = 346.5 cm^2`
Area of red region = Area of 2nd circle − Area of 1st circle
`=pir_2^2-pir_1^2`
`=pi(21)^2 - pi(10.5)^2`
= 441Π - 110.25Π = 330.75Π
= 1039.5 cm2
Area of blue region = Area of 3rd circle − Area of 2nd circle
`= pir_3^2 - pi_1^2`
`=pi(31.5)^2 -pi(21)^2`
`=992.25pi - 441pi = 551.25pi`
= 1732.5 cm2
Area of black region = Area of 4th circle − Area of 3rd circle
`= pir_4^2 - pir_3^2`
`=pi(42)^2-pi(31.5)^2`
`= 1764pi - 992.25pi`
Area of white region = Area of 5th circle − Area of 4th circle
`=pir_5^2 - pir_4^2`
`=pi(52.5)^2-pi(42)^2`
`= 2756.25pi - 1764pi`
`= 992.25pi = 3118.5 cm^2`
Therefore, areas of gold, red, blue, black, and white regions are 346.5 cm2, 1039.5 cm2, 1732.5 cm2, 2425.5 cm2, and 3118.5 cm2 respectively.
APPEARS IN
संबंधित प्रश्न
A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase, if he makes 2 rounds of fence. Also find the costs of the rope, if it cost ₹ 4 per meter. (Take `pi = 22/7`)
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that Perimeter of shaded region is 𝑟 (tan 𝜃 + sec 𝜃 +`(pitheta)/180`− 1)
The area of a minor sector of a circle is 3.85 cm2 and the measure of its central angle is 36°. Find the radius of the circle.
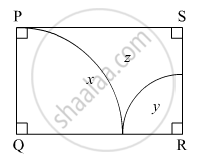
In the given figure,
\[\square\] PQRS is a rectangle. If PQ = 14 cm, QR = 21 cm, find the areas of the parts x, y, and z.
The sum of the circumference and diameter of a circle is 176 cm. Find the area of the circle.
Sudhanshu divides a circular disc of radius 7 cm in two equal parts. What is the perimeter of each semicircular shape disc? (Use π = `22/7`)
Diameters of different circles are given below. Find their circumference (Take π = `22/7`)
d = 56 m
A wire of length 1320 cm is made into circular frames of radius 7 cm each. How many frames can be made?
The area of a circle whose circumference is 22 cm, is ____________.
The circumference of a circle whose area is 81 πr2, is ______.
