Advertisements
Advertisements
प्रश्न
The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is traveling at a speed of 66 km per hour? [Use Π = 22/7]
उत्तर
Diameter of the wheel of the car = 80 cm
Radius (r) of the wheel of the car = 40 cm
Circumference of wheel = 2πr
= 2π (40) = 80π cm
Speed of car = 66 km/hour
= (66x100000)/60 cm/min
= 110000 cm/min
Distance travelled by the car in 10 minutes
= 110000 × 10 = 1100000 cm
Let the number of revolutions of the wheel of the car be n.
n × Distance travelled in 1 revolution (i.e., circumference)
= Distance travelled in 10 minutes
n x 80Π = 1100000
`n = (1100000xx7)/(80xx22)`
= (35000)/8 = 4375
Therefore, each wheel of the car will make 4375 revolutions.
APPEARS IN
संबंधित प्रश्न
The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
Find the circumference of the circle with the following radius: (Take `bb(pi = 22/7`)
28 mm
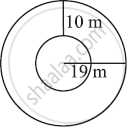
Find the circumference of the inner and the outer circles, shown in the adjoining figure? (Take π = 3.14)
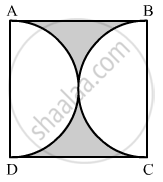
In the given figure, find the area of the shaded region, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
Four equal circles, each of radius a units, touch each other. Show that the area between them is `(6/7"a"^2)` sq units.
The diameter of a circle is 28 cm.
Find its :
(i) Circumference
(ii) Area.
In Figure 2, two concentric circles with centre O, have radii 21 cm and 42 cm. If ∠AOB = 60°, find the area of the shaded region.

The radius of a circle is 21 cm. Find the circumference (Take π = `3 1/7`).
In the formula, C = 2πr, ‘r’ refers to
The radii of the two circles are 19 cm and 9 cm respectively. The radius of the circle which has a circumference equal to the sum of the circumference of two circles is ____________.
