Advertisements
Advertisements
Question
Given figure depicts an archery target marked with its five scoring areas from the centre outwards as Gold, Red, Blue, Black and White. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions. [use π = 22/7]

Solution
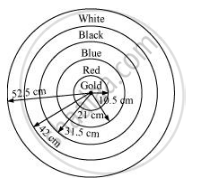
Radius (r1) of gold region (i.e., 1st circle) = 21/2 = 10.5 cm
Given that each circle is 10.5 cm wider than the previous circle.
Therefore, radius (r2) of 2nd circle = 10.5 + 10.5
21 cm
Radius (r3) of 3rd circle = 21 + 10.5
= 31.5 cm
Radius (r4) of 4th circle = 31.5 + 10.5
= 42 cm
Radius (r5) of 5th circle = 42 + 10.5
= 52.5 cm
Area of gold region = Area of 1st circle = `pir_1^2 = pi(10.5)^2 = 346.5 cm^2`
Area of red region = Area of 2nd circle − Area of 1st circle
`=pir_2^2-pir_1^2`
`=pi(21)^2 - pi(10.5)^2`
= 441Π - 110.25Π = 330.75Π
= 1039.5 cm2
Area of blue region = Area of 3rd circle − Area of 2nd circle
`= pir_3^2 - pi_1^2`
`=pi(31.5)^2 -pi(21)^2`
`=992.25pi - 441pi = 551.25pi`
= 1732.5 cm2
Area of black region = Area of 4th circle − Area of 3rd circle
`= pir_4^2 - pir_3^2`
`=pi(42)^2-pi(31.5)^2`
`= 1764pi - 992.25pi`
Area of white region = Area of 5th circle − Area of 4th circle
`=pir_5^2 - pir_4^2`
`=pi(52.5)^2-pi(42)^2`
`= 2756.25pi - 1764pi`
`= 992.25pi = 3118.5 cm^2`
Therefore, areas of gold, red, blue, black, and white regions are 346.5 cm2, 1039.5 cm2, 1732.5 cm2, 2425.5 cm2, and 3118.5 cm2 respectively.
APPEARS IN
RELATED QUESTIONS
Find the area of the sector of a circle whose radius is 14 cm and angle of sector is 45º
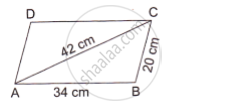
The adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm, and the diagonal AC measures 42 cm. Find the area of the parallelogram.
Find the area of the sector of a circle having radius 6 cm and of angle 30°. [Take π = 3.14]
In making 1000 revolutions, a wheel covers 88 km. The diameter of the wheel is
The wheel of the car makes 10 revolutions per second. If its diameter is 70 cm, find the speed of the car in km per hour.
The shaded portion of the figure, given alongside, shows two concentric circles. If the circumference of the two circles is 396 cm and 374 cm, find the area of the shaded portion.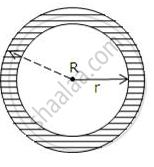
Find the radius and area of the circle which has circumference equal to the sum of circumferences of the two circles of radii 3 cm and 4 cm respectively.
In the formula, C = 2πr, ‘r’ refers to
Circumference of a circle is always ______.
A circle with radius 16 cm is cut into four equal parts and rearranged to form another shape as shown in the below figure:
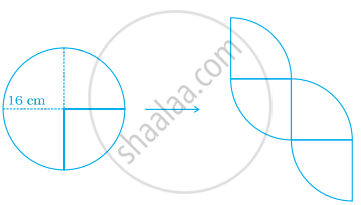
Does the perimeter change? If it does change, by how much does it increase or decrease?
