Advertisements
Advertisements
प्रश्न
How can you find the following?
Acceleration from velocity – time graph.
उत्तर
Acceleration from velocity – time graph: Velocity – time graph for uniform motion in a straight line (OP) inclined to the time axis.
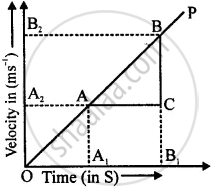
Take any two points A and B on this graph. From A and B draw perpendicular on the time axis as well as velocity axis in such a way that
OA1 = t1, OB1 = t2, OA2 = v1 and OB2 = v2
Slope of v – t graph = `"BC"/"AC"`
= `("v"_2-"v"_1)/("t"_2-"t"_1)=(Δ"v")/(Δ"t")` = Acceleration of the body
So, by knowing the slope of velocity – time graph for uniform motion, we can find the acceleration of the body.
APPEARS IN
संबंधित प्रश्न
Fill in the following blank with a suitable word:
Acceleration is the rate of change of ______ It is measured in ______
Find the initial velocity of a car which is stopped in 10 seconds by applying brakes. The retardation due to brakes is 2.5 m/s2.
Describe the motion of a body which is accelerating at a constant rate of 10 m s–2. If the body starts from rest, how much distance will it cover in 2 s ?
A cheetah starts from, rest, and accelerates at 2 m/s2 for 10 seconds. Calculate :
(a) the final velocity
(b) the distance travelled.
Give one example of following motion :
Variable acceleration
Derive the following equations for uniformly accelerated motion:
(i) v = u + at
(ii) `"S = ut" + 1/2 "at"^2`
(iii) v2 = u2 + 2aS
where the symbols have their usual meanings.
Multiple choice Question. Select the correct option.
At the maximum height, a body thrown vertically upwards has :
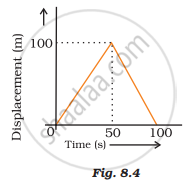
A girl walks along a straight path to drop a letter in the letterbox and comes back to her initial position. Her displacement–time graph is shown in Fig.8.4. Plot a velocity-time graph for the same.
The velocity-time graph (Fig. 8.5) shows the motion of a cyclist. Find (i) its acceleration (ii) its velocity and (iii) the distance covered by the cyclist in 15 seconds.

An electron moving with a velocity of 5 × 104 ms−1 enters into a uniform electric field and acquires a uniform acceleration of 104 ms–2 in the direction of its initial motion.
(i) Calculate the time in which the electron would acquire a velocity double of its initial velocity.
(ii) How much distance the electron would cover at this time?
