Advertisements
Advertisements
प्रश्न
Derive the following equations for uniformly accelerated motion:
(i) v = u + at
(ii) `"S = ut" + 1/2 "at"^2`
(iii) v2 = u2 + 2aS
where the symbols have their usual meanings.
उत्तर
Derivation of equations of motion
First equation of motion:
Consider a particle moving along a straight line with uniform acceleration 'a'. At t = 0, let the particle be at A and u be its initial velocity, and at t = t, let v be its final velocity.
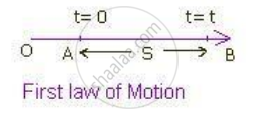
Acceleration = Change in velocity/Time a = (v - u)/t at = v - u
v = u+ at ... First equation of motion.
Second equation of motion: Average velocity = Total distance traveled/Total time taken Average velocity = s/t ...(1)
Average velocity can be written as (u+v)/2 Average velocity = (u+v)/2 ...(2)
From equations (1) and (2) s/t = (u+v)/2 ...(3)
The first equation of motion is v = u + at.
Substituting the value of v in equation (3), we get
s/t = (u + u + at)/2 s = (2u + at) t/2 = 2ut + at2/2 = 2ut/2 + at2/2
s = ut + (1/2) at2 …Second equation of motion.
Third equation of motion: The first equation of motion is v = u + at. v - u = at ... (1)
Average velocity = s/t ...(2)
Average velocity =(u+v)/2 ...(3)
From equation (2) and equation (3) we get,
(u + v)/2 = s/t ...(4)
Multiplying eq (1) and eq (4) we get,
(v - u)(v + u) = at × (2s/t) (v - u)(v + u) = 2as
[We make the use of the identity a2 - b2 = (a + b) (a - b)]
v2 - u2 = 2as ...Third equation of motion.
APPEARS IN
संबंधित प्रश्न
A bus was moving with a speed of 54 km/h. On applying brakes it stopped in 8 seconds. Calculate the acceleration.
A freely falling object travels 4.9 m in 1st second, 14.7 m in 2 nd second, 24.5 m in 3rd second, and so on. This data shows that the motion of a freely falling object is a case of :
The slope of a speed-time graph gives:
The velocity-time graph of a body in motion is a straight line inclined to the time axis. The correct statement is ___________
A body, initially at rest, starts moving with a constant acceleration 2 m s-2. Calculate: (i) the velocity acquired and (ii) the distance travelled in 5 s.
When is the negative acceleration?
How can you find the following?
Velocity from acceleration – time graph.
Can you suggest a real-life example about the motion of a body from the following velocity – time graph?
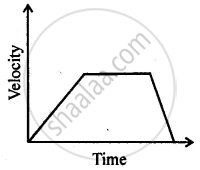
Can you suggest a real-life example about the motion of a body from the following velocity – time graph?
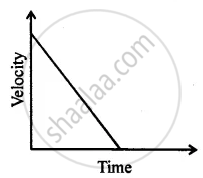
How will the equations of motion for an object moving with a uniform velocity change?
