Advertisements
Advertisements
प्रश्न
How can you find the following?
Velocity from acceleration – time graph.
Advertisements
उत्तर
Velocity from acceleration – time graph: Area under the acceleration – time graph gives the velocity of the body. When the body moves with variable velocity but uniform acceleration, then acceleration – time graph is a straight line (PQ) parallel to the time axis.
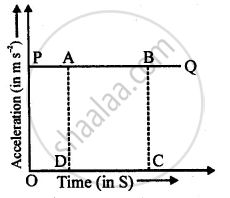
Take any two points A and B on PQ. From P and Q, draw perpendiculars (BC and AD) on the time axis. such that,
OD = t1 and OC = t2
Let OP = AD = BC = a = acceleration of the body.
Area under acceleration – time graph = area of rectangle ABCD
= AD × DC = AD × (OC − OD)
= a (t2 − t1)
= `("v"-"u")/(("t"_2-"t"_1))("t"_2-"t"_1)` = v − u
If initial velocity of the body = u = 0 Then area under acceleration – time graph = v – 0 = v = velocity of the body.
APPEARS IN
संबंधित प्रश्न
A train starting from a railway station and moving with uniform acceleration attains a speed 40 km h−1 in 10 minutes. Find its acceleration.
Which of the two can be zero under certain conditions : average speed of a moving body or average velocity of a moving body ?
Fill in the following blank with suitable word :
If a body moves with uniform velocity, its acceleration is ..............
A cheetah starts from, rest, and accelerates at 2 m/s2 for 10 seconds. Calculate :
(a) the final velocity
(b) the distance travelled.
A train starting from stationary position and moving with uniform acceleration attains a speed of 36 km per hour in 10 minutes. Find its acceleration.
If a stone and a pencil are dropped simultaneously in vacuum from the top of a tower, then which of the two will reach the ground first? Give reason.
What do you understand by the term acceleration?
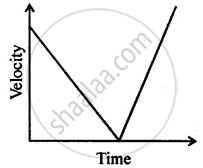
Can you suggest a real-life example about the motion of a body from the following velocity – time graph?
The velocity-time graph (Fig. 8.5) shows the motion of a cyclist. Find (i) its acceleration (ii) its velocity and (iii) the distance covered by the cyclist in 15 seconds.
An electron moving with a velocity of 5 × 104 ms−1 enters into a uniform electric field and acquires a uniform acceleration of 104 ms–2 in the direction of its initial motion.
(i) Calculate the time in which the electron would acquire a velocity double of its initial velocity.
(ii) How much distance the electron would cover at this time?
