Advertisements
Advertisements
Question
How can you find the following?
Velocity from acceleration – time graph.
Solution
Velocity from acceleration – time graph: Area under the acceleration – time graph gives the velocity of the body. When the body moves with variable velocity but uniform acceleration, then acceleration – time graph is a straight line (PQ) parallel to the time axis.
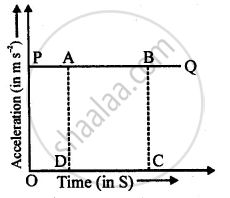
Take any two points A and B on PQ. From P and Q, draw perpendiculars (BC and AD) on the time axis. such that,
OD = t1 and OC = t2
Let OP = AD = BC = a = acceleration of the body.
Area under acceleration – time graph = area of rectangle ABCD
= AD × DC = AD × (OC − OD)
= a (t2 − t1)
= `("v"-"u")/(("t"_2-"t"_1))("t"_2-"t"_1)` = v − u
If initial velocity of the body = u = 0 Then area under acceleration – time graph = v – 0 = v = velocity of the body.
APPEARS IN
RELATED QUESTIONS
Fill in the following blank with a suitable word:
Acceleration is the rate of change of ______ It is measured in ______
Define velocity. What is the SI unit of velocity ?
A cheetah starts from, rest, and accelerates at 2 m/s2 for 10 seconds. Calculate :
(a) the final velocity
(b) the distance travelled.
A car is travelling along the road at 8 ms-1. It accelerates at 1 ms-2 for a distance of 18 m. How fast is it then travelling ?
Write three equations of uniformly accelerated motion relating the initial velocity (u), final velocity (v), time (t), acceleration (a) and displacement (S).
Can you suggest a real-life example about the motion of a body from the following velocity – time graph?
A stone thrown vertically upwards takes 3 s to attain maximum height. Calculate
- initial velocity of the stone
- maximum height attained by the stone. (Take g = 9.8 ms−2)
The velocity-time graph (Fig. 8.5) shows the motion of a cyclist. Find (i) its acceleration (ii) its velocity and (iii) the distance covered by the cyclist in 15 seconds.

Draw a velocity versus time graph of a stone thrown vertically upwards and then coming downwards after attaining the maximum height.
Two stones are thrown vertically upwards simultaneously with their initial velocities u1 and u2 respectively. Prove that the heights reached by them would be in the ratio of `"u"_1^2 : "u"_2^2` (Assume upward acceleration is –g and downward acceleration to be +g)
