Question

How can you find the following?

Velocity from acceleration – time graph.

Answer 1

Velocity from acceleration – time graph: Area under the acceleration – time graph gives the velocity of the body. When the body moves with variable velocity but uniform acceleration, then acceleration – time graph is a straight line (PQ) parallel to the time axis.

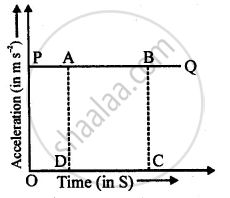
Take any two points A and B on PQ. From P and Q, draw perpendiculars (BC and AD) on the time axis. such that,
OD = t₁ and OC = t₂
Let OP = AD = BC = a = acceleration of the body.
Area under acceleration – time graph = area of rectangle ABCD
= AD × DC = AD × (OC − OD)
= a (t₂ − t₁)
= `("v"-"u")/(("t"_2-"t"_1))("t"_2-"t"_1)` = v − u

If initial velocity of the body = u = 0 Then area under acceleration – time graph = v – 0 = v = velocity of the body.