Advertisements
Advertisements
प्रश्न
Derive the following equations for uniformly accelerated motion:
(i) v = u + at
(ii) `"S = ut" + 1/2 "at"^2`
(iii) v2 = u2 + 2aS
where the symbols have their usual meanings.
उत्तर
Derivation of equations of motion
First equation of motion:
Consider a particle moving along a straight line with uniform acceleration 'a'. At t = 0, let the particle be at A and u be its initial velocity, and at t = t, let v be its final velocity.
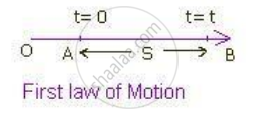
Acceleration = Change in velocity/Time a = (v - u)/t at = v - u
v = u+ at ... First equation of motion.
Second equation of motion: Average velocity = Total distance traveled/Total time taken Average velocity = s/t ...(1)
Average velocity can be written as (u+v)/2 Average velocity = (u+v)/2 ...(2)
From equations (1) and (2) s/t = (u+v)/2 ...(3)
The first equation of motion is v = u + at.
Substituting the value of v in equation (3), we get
s/t = (u + u + at)/2 s = (2u + at) t/2 = 2ut + at2/2 = 2ut/2 + at2/2
s = ut + (1/2) at2 …Second equation of motion.
Third equation of motion: The first equation of motion is v = u + at. v - u = at ... (1)
Average velocity = s/t ...(2)
Average velocity =(u+v)/2 ...(3)
From equation (2) and equation (3) we get,
(u + v)/2 = s/t ...(4)
Multiplying eq (1) and eq (4) we get,
(v - u)(v + u) = at × (2s/t) (v - u)(v + u) = 2as
[We make the use of the identity a2 - b2 = (a + b) (a - b)]
v2 - u2 = 2as ...Third equation of motion.
APPEARS IN
संबंधित प्रश्न
Which of the two can be zero under certain conditions : average speed of a moving body or average velocity of a moving body ?
A train travelling at 20 m s-1 accelerates at 0.5 m s-2 for 30 s. How far will it travel in this time ?
A boy is sitting on a merry-go-round which is moving with a constant speed of 10 m s−1. This means that the boy is :
When a car driver travelling at a speed of 10 m/s applies brakes and brings the car to rest in 20 s, then retardation will be :
A bus increases its speed from 36 km/h to 72 km/h in 10 seconds. Its acceleration is :
The slope of a speed-time graph gives:
Write three equations of uniformly accelerated motion relating the initial velocity (u), final velocity (v), time (t), acceleration (a) and displacement (S).
What do you understand by the term acceleration?
Can you suggest a real-life example about the motion of a body from the following velocity – time graph?
The velocity-time graph (Fig. 8.5) shows the motion of a cyclist. Find (i) its acceleration (ii) its velocity and (iii) the distance covered by the cyclist in 15 seconds.

