Advertisements
Advertisements
Question
Derive the following equations for uniformly accelerated motion:
(i) v = u + at
(ii) `"S = ut" + 1/2 "at"^2`
(iii) v2 = u2 + 2aS
where the symbols have their usual meanings.
Solution
Derivation of equations of motion
First equation of motion:
Consider a particle moving along a straight line with uniform acceleration 'a'. At t = 0, let the particle be at A and u be its initial velocity, and at t = t, let v be its final velocity.
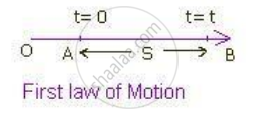
Acceleration = Change in velocity/Time a = (v - u)/t at = v - u
v = u+ at ... First equation of motion.
Second equation of motion: Average velocity = Total distance traveled/Total time taken Average velocity = s/t ...(1)
Average velocity can be written as (u+v)/2 Average velocity = (u+v)/2 ...(2)
From equations (1) and (2) s/t = (u+v)/2 ...(3)
The first equation of motion is v = u + at.
Substituting the value of v in equation (3), we get
s/t = (u + u + at)/2 s = (2u + at) t/2 = 2ut + at2/2 = 2ut/2 + at2/2
s = ut + (1/2) at2 …Second equation of motion.
Third equation of motion: The first equation of motion is v = u + at. v - u = at ... (1)
Average velocity = s/t ...(2)
Average velocity =(u+v)/2 ...(3)
From equation (2) and equation (3) we get,
(u + v)/2 = s/t ...(4)
Multiplying eq (1) and eq (4) we get,
(v - u)(v + u) = at × (2s/t) (v - u)(v + u) = 2as
[We make the use of the identity a2 - b2 = (a + b) (a - b)]
v2 - u2 = 2as ...Third equation of motion.
APPEARS IN
RELATED QUESTIONS
When will you say a body is at non-uniform acceleration?
Give one example of a situation in which a body has a certain average speed but its average velocity is zero.
Derive the formula : v = u + at, where the symbols have usual meanings.
When a car driver travelling at a speed of 10 m/s applies brakes and brings the car to rest in 20 s, then retardation will be :
A body, initially at rest, starts moving with a constant acceleration 2 m s-2. Calculate: (i) the velocity acquired and (ii) the distance travelled in 5 s.
How can you find the following?
Velocity from acceleration – time graph.
Can you suggest a real-life example about the motion of a body from the following velocity – time graph?
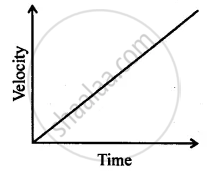
Can you suggest a real-life example about the motion of a body from the following velocity – time graph?
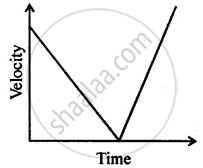
A packet is dropped from a stationary helicopter, hovering at a height ‘h’ from ground level, reaches the ground in 12s. Calculate
- the value of h
- final velocity of packet on reaching the ground. (Take g = 9.8 ms−2)
A body is thrown vertically upward with velocity u, the greatest height h to which it will rise is,
