Advertisements
Advertisements
प्रश्न
How many 1s energy states are present in one mole of sodium vapour? Are they all filled in normal conditions? How many 3s energy states are present in one mole of sodium vapour? Are they all filled in normal conditions?
उत्तर
For sodium, the atomic number is 11. The electronic configuration of sodium is 1s2 2s22p6 3s1.
One sodium atom has 11 electrons. Thus, if the sodium crystals consist of N atoms, the total number of electrons will be 11 N. We know that for each atom, there are two states in the energy level 1s. Thus, the sodium crystal will have 2 N states for 1s energy level. Similarly, the number of states in 3s energy level will also be 2 N. 1s state is filled under normal condition. But the 3s state has only one electron per sodium atom, so the 3s band will be half-filled.
APPEARS IN
संबंधित प्रश्न
Distinguish between a conductor and a semi conductor on the basis of energy band diagram
Write two characteristic features to distinguish between n-type and p-type semiconductors ?
In semiconductors, thermal collisions are responsible for taking a valence electron to the conduction band. Why does the number of conduction electrons not go on increasing with time as thermal collisions continuously take place?
Let np and ne be the number of holes and conduction electrons in an intrinsic semiconductor.
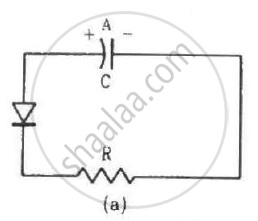
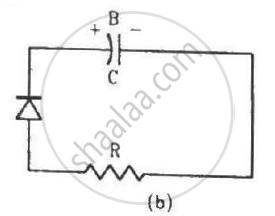
Two identical capacitors A and B are charged to the same potential V and are connected in two circuits at t = 0 as shown in figure. The charges on the capacitors at a time t = CRare, respectively,
In a transistor,
An incomplete sentence about transistors is given below:
The emitter−..... junction is __ and the collector−..... junction is __. The appropriate words for the dotted empty positions are, respectively,
Calculate the number of states per cubic metre of sodium in 3s band. The density of sodium is 1013 kgm−3. How many of them are empty?
The band gap between the valence and the conduction bands in zinc oxide (ZnO) is 3.2 eV. Suppose an electron in the conduction band combines with a hole in the valence band and the excess energy is released in the form of electromagnetic radiation. Find the maximum wavelength that can be emitted in this process.
Estimate the proportion of boron impurity which will increase the conductivity of a pure silicon sample by a factor of 100. Assume that each boron atom creates a hole and the concentration of holes in pure silicon at the same temperature is 7 × 1015 holes per cubic metre. Density of silicon 5 × 1028 atoms per cubic metre.
The conductivity of an intrinsic semiconductor depends on temperature as σ = σ0e−ΔE/2kT, where σ0 is a constant. Find the temperature at which the conductivity of an intrinsic germanium semiconductor will be double of its value at T = 300 K. Assume that the gap for germanium is 0.650 eV and remains constant as the temperature is increased.
(Use Planck constant h = 4.14 × 10-15 eV-s, Boltzmann constant k = 8·62 × 10-5 eV/K.)
A semiconducting material has a band gap of 1 eV. Acceptor impurities are doped into it which create acceptor levels 1 meV above the valence band. Assume that the transition from one energy level to the other is almost forbidden if kT is less than 1/50 of the energy gap. Also if kT is more than twice the gap, the upper levels have maximum population. The temperature of the semiconductor is increased from 0 K. The concentration of the holes increases with temperature and after a certain temperature it becomes approximately constant. As the temperature is further increased, the hole concentration again starts increasing at a certain temperature. Find the order of the temperature range in which the hole concentration remains approximately constant.
(Use Planck constant h = 4.14 × 10-15 eV-s, Boltzmann constant k = 8·62 × 10-5 eV/K.)
With reference to Semiconductor Physics,
Draw a labelled energy band diagram for a semiconductor.
The energy of a hydrogen atom in the ground state is −13.6 eV. The energy of a He+ ion in the first excited state will be:
For germanium crystal, the forbidden gas energy gap
The reaction between α and β parameter of a transistor is given by
Hole are majority charge carrier in
Three photo diodes D1, D2 and D3 are made of semiconductors having band gaps of 2.5 eV, 2 eV and 3 eV, respectively. Which 0 ones will be able to detect light of wavelength 6000 Å?
Which one of the following elements will require the highest energy to take out an electron from them?
Pb, Ge, C and Si
With reference to semiconductor physics, answer the following question.
What is meant by “Forbidden band" of energy levels?
