Advertisements
Advertisements
प्रश्न
Identical springs of steel and copper are equally stretched. On which, more work will have to be done?
उत्तर
Work Done in stretching a Wire or Spring: In stretching a wire work is done against internal restoring forces. This work is stored in the wire as elastic potential energy or strain energy.
If a force F acts along the length L of the wire of cross-section A and stretches it by x, then work done in stretching a wire is given by W = 1/2F × Δl
As springs of steel and copper are equally stretched. Therefore, for the same force (F),
`W ∝ Δl` ......(i)
Young's modulus `(Y) = F/A xx l/(Δl)`
or `Δl = F/A xx l/Y`
As both springs are identical,
∴ `Δl ∝ 1/Y` ......(ii)
From equations (i) and (ii), we get `W ∝ 1/Y`
∴ `W_(steel)/W_(copper) = Y_(copper)/(Y_(steel)) > 1` ......(As `Y_(steel) > Y_(copper)`)
or `W_(steel) > W_(copper)`
Therefore, more work will be done for stretching copper spring.
APPEARS IN
संबंधित प्रश्न
A steel wire of length 4.7 m and cross-sectional area 3.0 × 10–5 m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4.0 × 10–5 m2 under a given load. What is the ratio of Young’s modulus of steel to that of copper?
Four identical hollow cylindrical columns of mild steel support a big structure of mass 50,000 kg. The inner and outer radii of each column are 30 cm and 60 cm respectively. Assuming the load distribution to be uniform, calculate the compressional strain of each column.
A 14.5 kg mass, fastened to the end of a steel wire of unstretched length 1.0 m, is whirled in a vertical circle with an angular velocity of 2 rev/s at the bottom of the circle. The cross-sectional area of the wire is 0.065 cm2. Calculate the elongation of the wire when the mass is at the lowest point of its path.
The length of a metal wire is l1 when the tension in it T1 and is l2 when the tension is T2. The natural length of the wire is
A copper wire of cross-sectional area 0.01 cm2 is under a tension of 20N. Find the decrease in the cross-sectional area. Young modulus of copper = 1.1 × 1011 N m−2 and Poisson ratio = 0.32.
`["Hint" : (Delta"A")/"A"=2(Delta"r")/"r"]`
A uniform rectangular block of mass of 50 kg is hung horizontally with the help of three wires A, B and C each of length and area of 2m and 10mm2 respectively as shown in the figure. The central wire is passing through the centre of gravity and is made of material of Young's modulus 7.5 x 1010 Nm−2 and the other two wires A and C symmetrically placed on either side of the wire B are of Young's modulus 1011 Nm−2 The tension in the wires A and B will be in the ratio of:
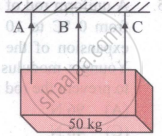
A rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to ______.
The Young’s modulus for steel is much more than that for rubber. For the same longitudinal strain, which one will have greater tensile stress?
A steel rod (Y = 2.0 × 1011 Nm–2; and α = 10–50 C–1) of length 1 m and area of cross-section 1 cm2 is heated from 0°C to 200°C, without being allowed to extend or bend. What is the tension produced in the rod?
A uniform metal rod of 2 mm2 cross section is heated from 0°C to 20°C. The coefficient of linear expansion of the rod is 12 × 10-6/°C, it's Young's modulus is 1011 N/m2. The energy stored per unit volume of the rod is ______.
