Advertisements
Advertisements
प्रश्न
A rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to ______.
विकल्प
`Y_(copper)/Y_(iron)`
`sqrt((Y_(iron))/(Y_(copper)`
`Y_(iron)^2/Y_(copper)^2`
`Y_(iron)/Y_(copper)^2`
उत्तर
A rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to `underline(sqrt((Y_(iron))/(Y_(copper))`.
Explanation:
As the bar is supported symmetrically by the three wires, therefore extension in each wire is the same.
Let T be the tension in each wire and the diameter of the wire is D, then Young’s modulus is `Y = "Stress"/"Strain"`
= `(F/A)/((ΔL)/L)`
= `F/A xx L/(ΔL)`
= `F/(pi(D/2)^2) xx L/(ΔL)`
= `(4FL)/(piD^2ΔL)`
⇒ `D^2 = (4FL)/(piΔLY)`
⇒ `D = sqrt((4FL)/(piΔLY)`
As F and `L/(ΔL)` are constants.
Hence, `D ∝ sqrt(1/Y)`
or `D = K/sqrt(Y)` ......(K is the proportionality constant)
Now, we can find ratio as `D_(copper)/D_(iron) = sqrt(Y_(iron)/Y_(copper)`
APPEARS IN
संबंधित प्रश्न
Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in Fig. 9.13. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires.

The length of a metal wire is l1 when the tension in it T1 and is l2 when the tension is T2. The natural length of the wire is
A student plots a graph from his reading on the determination of Young modulus of a metal wire but forgets to put the labels. the quantities on X and Y-axes may be respectively
(a) weight hung and length increased
(b) stress applied and length increased
(c) stress applied and strain developed
(d) length increased and the weight hung.
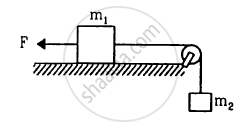
Consider the situation shown in figure. The force F is equal to the m2 g/2. If the area of cross section of the string is A and its Young modulus Y, find the strain developed in it. The string is light and there is no friction anywhere.
Young's modulus of a perfectly rigid body is ______.
Identical springs of steel and copper are equally stretched. On which, more work will have to be done?
A steel rod (Y = 2.0 × 1011 Nm–2; and α = 10–50 C–1) of length 1 m and area of cross-section 1 cm2 is heated from 0°C to 200°C, without being allowed to extend or bend. What is the tension produced in the rod?
A truck is pulling a car out of a ditch by means of a steel cable that is 9.1 m long and has a radius of 5 mm. When the car just begins to move, the tension in the cable is 800 N. How much has the cable stretched? (Young’s modulus for steel is 2 × 1011 Nm–2.)
A boy's catapult is made of rubber cord which is 42 cm long, with a 6 mm diameter of cross-section and negligible mass. The boy keeps a stone weighing 0.02 kg on it and stretches the cord by 20 cm by applying a constant force. When released, the stone flies off with a velocity of 20 ms-1. Neglect the change in the area of the cross-section of the cord while stretched. Young's modulus of rubber is closest to ______.
If the length of a wire is made double and the radius is halved of its respective values. Then, Young's modules of the material of the wire will ______.
