Advertisements
Advertisements
प्रश्न
A rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to ______.
पर्याय
`Y_(copper)/Y_(iron)`
`sqrt((Y_(iron))/(Y_(copper)`
`Y_(iron)^2/Y_(copper)^2`
`Y_(iron)/Y_(copper)^2`
उत्तर
A rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to `underline(sqrt((Y_(iron))/(Y_(copper))`.
Explanation:
As the bar is supported symmetrically by the three wires, therefore extension in each wire is the same.
Let T be the tension in each wire and the diameter of the wire is D, then Young’s modulus is `Y = "Stress"/"Strain"`
= `(F/A)/((ΔL)/L)`
= `F/A xx L/(ΔL)`
= `F/(pi(D/2)^2) xx L/(ΔL)`
= `(4FL)/(piD^2ΔL)`
⇒ `D^2 = (4FL)/(piΔLY)`
⇒ `D = sqrt((4FL)/(piΔLY)`
As F and `L/(ΔL)` are constants.
Hence, `D ∝ sqrt(1/Y)`
or `D = K/sqrt(Y)` ......(K is the proportionality constant)
Now, we can find ratio as `D_(copper)/D_(iron) = sqrt(Y_(iron)/Y_(copper)`
APPEARS IN
संबंधित प्रश्न
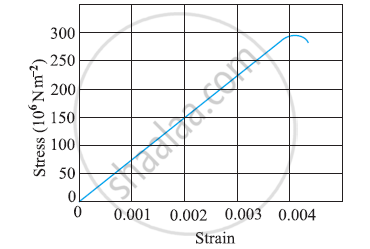
The figure shows the strain-stress curve for a given material. What are (a) Young’s modulus and (b) approximate yield strength for this material?
The length of a metal wire is l1 when the tension in it T1 and is l2 when the tension is T2. The natural length of the wire is
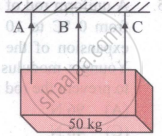
A uniform rectangular block of mass of 50 kg is hung horizontally with the help of three wires A, B and C each of length and area of 2m and 10mm2 respectively as shown in the figure. The central wire is passing through the centre of gravity and is made of material of Young's modulus 7.5 x 1010 Nm−2 and the other two wires A and C symmetrically placed on either side of the wire B are of Young's modulus 1011 Nm−2 The tension in the wires A and B will be in the ratio of:
Young's modulus of a perfectly rigid body is ______.
What is the Young’s modulus for a perfect rigid body ?
A truck is pulling a car out of a ditch by means of a steel cable that is 9.1 m long and has a radius of 5 mm. When the car just begins to move, the tension in the cable is 800 N. How much has the cable stretched? (Young’s modulus for steel is 2 × 1011 Nm–2.)
A steel wire of mass µ per unit length with a circular cross section has a radius of 0.1 cm. The wire is of length 10 m when measured lying horizontal, and hangs from a hook on the wall. A mass of 25 kg is hung from the free end of the wire. Assuming the wire to be uniform and lateral strains << longitudinal strains, find the extension in the length of the wire. The density of steel is 7860 kg m–3 (Young’s modules Y = 2 × 1011 Nm–2).
If the yield strength of steel is 2.5 × 108 Nm–2, what is the maximum weight that can be hung at the lower end of the wire?
A metal wire of length L, area of cross section A and Young's modulus Y behaves as a spring of spring constant k given by:
A uniform metal rod of 2 mm2 cross section is heated from 0°C to 20°C. The coefficient of linear expansion of the rod is 12 × 10-6/°C, it's Young's modulus is 1011 N/m2. The energy stored per unit volume of the rod is ______.
