Advertisements
Advertisements
प्रश्न
If \[\overline{{3x2}}\] is a multiple of 11, where x is a digit, what is the value of x?
उत्तर
\[\text{ Sum of the digits at odd places }= 3 + 2 = 5\]
Sum of the digit at even place = x
\[ \therefore\text{ Sum of the digit at even place - Sum of the digits at odd places }= (x - 5)\]
\[ \because (x - 5) \text{ must be multiple by }11 . \]
\[ \therefore\text{ Possible values of }(x - 5)\text{ are }0, 11, 22, 33 . . . \]
\[\text{ But }x\text{ is a digit; therefore }x\text{ must be }0, 1 , 2, 3 . . . 9 . \]
\[ \therefore x - 5 = 0 \]
\[ \Rightarrow x = 5\]
APPEARS IN
संबंधित प्रश्न
Look at the patterns of numbers in hexagons.
Each side has 2 circles and 1 box.
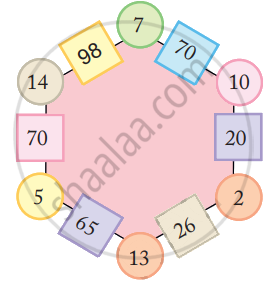
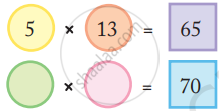
- Look at the number 65 in the box. Which are the circles next to it?
- Can you see how the rule works?
Fill in the blank space in the same way.

Now you try and change these numbers into special numbers —
132
20 × 3 is a multiple of 3 if the digit × is ______ or ______ or ______.
If 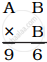 then A = ______ and B = ______.
then A = ______ and B = ______.
A four-digit number abcd is divisible by 11, if d + b = ______ or _____.
A number is divisible by 11 if the differences between the sum of digits at its odd places and that of digits at the even places is either 0 or divisible by ______.
A four-digit number abcd is divisible by 4 if ab is divisible by 4.
If 148101B095 is divisible by 33, find the value of B.
If 123123A4 is divisible by 11, find the value of A.
