Advertisements
Advertisements
प्रश्न
If 3x = a + b + c, then the value of (x − a)3 + (x −b)3 + (x − c)3 − 3(x − a) (x − b) (x −c) is
विकल्प
a + b + c
(a − b) (b − c) (c − a)
0
none of these
उत्तर
The given expression is
(x − a)3 + (x −b)3 + (x − c)3 − 3(x − a) (x − b) (x −c)
Recall the formula
`a^3 +b^3 +c^3 - 3abc = (a+b+c)(a^2 + b^2+ c^2 - ab - bc +_ ca)`
Using the above formula the given expression becomes
(x − a)3 + (x −b)3 + (x − c)3 − 3(x − a) (x − b) (x −c)
`{(x-a) +(x-b) + (x-c)} {(x-a)^2+(x-b)^2+(x-c)^2 -(x-a)(x-b)-(x-b)(x-c) - (x-c)(x-a)}`
`(x-a +x-b+x -c) {(x-a)^2+(x-b)^2+(x-c)^2 -(x-a)(x-b)-(x-b)(x-c) - (x-c)(x-a)} `
`(3x-a -b-c) {(x-a)^2+(x-b)^2+(x-c)^2 -(x-a)(x-b)-(x-b)(x-c) - (x-c)(x-a)}`
Given that
`3x = (a+b+c)`
` ⇒ 3x -a-b-c =0`
Therefore the value of the given expression is
(x − a)3 + (x −b)3 + (x − c)3 − 3(x − a) (x − b) (x −c)
`= 0.{(x-a)^2+(x-b)^2+(x-c)^2 -(x-a)(x-b)-(x-b)(x-c) - (x-c)(x-a)}`
`=0`
APPEARS IN
संबंधित प्रश्न
Factorize the following expressions:
1029 – 3x3
x3 - 8y3 + 27z3 +18xyz
Multiply: x2 + y2 + z2 − xy + xz + yz by x + y − z
(x + y)3 − (x − y)3 can be factorized as
Mark the correct alternative in each of the following: The factors of a2 − 1 − 2x − x2 are
Multiply: (1 + 6x2 - 4x3)(-1 + 3x - 3x2)
Divide: 9x2 - 24xy + 16y2 by 3x- 4y
Divide: 5x2 - 3x by x
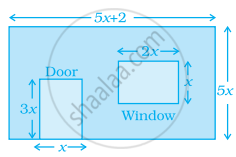
The figure shows the dimensions of a wall having a window and a door of a room. Write an algebraic expression for the area of the wall to be painted.
–b – 0 is equal to ______.
