Advertisements
Advertisements
प्रश्न
If ∝ and β are the zeros of the polynomial f(x) = `6x^2 + x - 2 `find the value of `(∝/β+∝/β) `
उत्तर
By using the relationship between the zeroes of the quadratic polynomial.
We have
Sum of zeroes=`(-("Coefficent of x"))/("Coefficient of" x^2)` and Product of zeroes = `"Constant term"/("Coefficient of" x^2)`
∴ 𝛼 + 𝛽=`-1/6` and 𝛼𝛽 =`-1/3`
Now, `∝/β+β/∝=(∝^2+β^2)/(∝β)`
`= (∝^2+β^2+2∝β-2∝β)/(∝β)`
`=((∝+β)^2-2∝β)/(∝β)`
`=((-1/6)^2-2(1/3))/(1/3)`
`=(1/36+2/3)/ (1/3)`
`=-25/12`
APPEARS IN
संबंधित प्रश्न
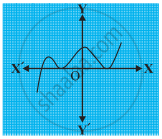
The graphs of y = p(x) are given in following figure, for some polynomials p(x). Find the number of zeroes of p(x).
Find the zeroes of the quadratic polynomial `f(x) = x^2 + 3x ˗ 10` and verify the relation between its zeroes and coefficients.
Write the zeros of the polynomial `f(x) = x^2 – x – 6`.
Find the sum of the zeros and the product of zeros of a quadratic polynomial, are `−1/2` and \ -3 respectively. Write the polynomial.
If 𝛼, 𝛽 are the zeroes of the polynomial `f(x) = x^2 – 5x + k` such that 𝛼 - 𝛽 = 1, find the value of k = ?
If one zero of the quadratic polynomial x2 + 3x + k is 2, then the value of k is ______.
If one of the zeroes of the quadratic polynomial (k – 1) x2 + kx + 1 is - 3, then the value of k is ______.
A quadratic polynomial, whose zeroes are -3 and 4, is ______.
The number of polynomials having zeroes as -2 and 5 is ______.
If p(x) is a polynomial of at least degree one and p(k) = 0, then k is known as ______.
