Advertisements
Advertisements
प्रश्न
Find the zeroes of the quadratic polynomial `f(x) = x^2 + 3x ˗ 10` and verify the relation between its zeroes and coefficients.
उत्तर
We have:
`f(x) = x^2 + 3x ˗ 10`
=` x^2 + 5x ˗ 2x ˗ 10`
= x(x + 5) ˗ 2(x + 5)
= (x ˗ 2) (x + 5)
∴ f(x) = 0 ⇒ (x ˗ 2) (x + 5) = 0
⇒ x ˗ 2 = 0 or x + 5 = 0
⇒ x = 2 or x = −5.
So, the zeroes of f(x) are 2 and −5.
Sum of zeroes= `2+(-5)=-3=(-3)/1="(-coefficient of x)" /(("Coefficent of "x^2))`
Product of zeroes =`2xx(-5)=-10=(-10)/1= "Constant term"/(("Coefficcient of "x^2 ))`
APPEARS IN
संबंधित प्रश्न
Find all the zeroes of `(2x^4 – 3x^3 – 5x2 + 9x – 3)`, it is being given that two of its zeroes are `sqrt3 and –sqrt3`.
Find the zeroes of the polynomial `x^2 – 3x – m(m + 3)`
If -2 is a zero of the polynomial `3x^2 + 4x + 2k` then find the value of k.
Find the zeroes of the quadratic polynomial `f(x) = 6x^2 – 3.`
Find the value of k such that the polynomial x2 − (k + 6)x + 2(2k −1) has sum of its zeros equal to half of their product.
If x4 + 3x2 + 7 is divided by 3x + 5, then the possible degrees of quotient and remainder are ______.
If the zeroes of the quadratic polynomial ax2 + bx + c, c ≠ 0 are equal, then ______.
If α and β are the zeroes of the polynomial x2 – 1, then the value of (α + β) is ______.
The number of polynomials having zeroes – 3 and 4 is ______.
The graph of y = f(x) is shown in the figure for some polynomial f(x).
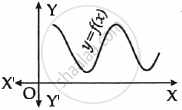
The number of zeroes of f(x) is ______.
