Advertisements
Advertisements
प्रश्न
If l, m, n are three lines such that l || m and n ⊥ l, prove that n ⊥ m.
उत्तर

Given l || , m ,n perpendicular l
To prove: n ⊥ m
Since l || m and n intersects them at G and H respectively
∴`∠`1= `∠`2 [Corresponding angles]
But, U = 90° [n ⊥ l ]
⇒ `∠`2 = 90°
Hence n perpendicular m
APPEARS IN
संबंधित प्रश्न
How many pairs of adjacent angles are formed when two lines intersect in a point?
In the below fig, lines �1 and �2 intersect at O, forming angles as shown in the figure. If x = 45, Find the values of x, y, z and u.
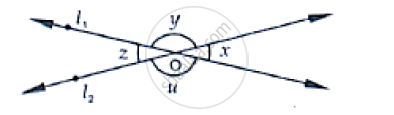
In the below fig, three coplanar lines intersect at a point O, forming angles as shown in the figure. Find the values of x, y, z and u.

Prove that the bisectors of a pair of vertically opposite angles are in the same straight line.
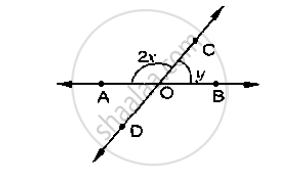
In the below fig, rays AB and CD intersect at O
Determine x when y =40
Two straight line AB and CD intersect one another at the point O. If ∠AOC + ∠COB + ∠BOD = 274°, then ∠AOD =
In the given figure, the value of y is
Two lines are respectively perpendicular to two parallel lines. Show that they are parallel to each other.
Two parallel lines meet each other at some point.
Two lines in a plane which do not meet at a point anywhere are called ______ lines.
