Advertisements
Advertisements
प्रश्न
If l, m, n are three lines such that l || m and n ⊥ l, prove that n ⊥ m.
उत्तर

Given l || , m ,n perpendicular l
To prove: n ⊥ m
Since l || m and n intersects them at G and H respectively
∴`∠`1= `∠`2 [Corresponding angles]
But, U = 90° [n ⊥ l ]
⇒ `∠`2 = 90°
Hence n perpendicular m
APPEARS IN
संबंधित प्रश्न
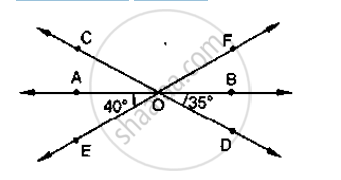
In the below fig, lines AB, CD and EF intersect at O. Find the measures of ∠AOC, ∠COF,
∠DOE and ∠BOF.
Two straight line AB and CD intersect one another at the point O. If ∠AOC + ∠COB + ∠BOD = 274°, then ∠AOD =
Consider the following statements:
When two straight lines intersect:
(i) adjacent angles are complementary
(ii) adjacent angles are supplementary
(iii) opposite angles are equal
(iv) opposite angles are supplementary
Of these statements
Given ∠POR = 3x and ∠QOR = 2x + 10°. If POQ is a straight line, then the value of x is
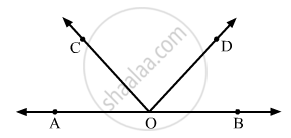
In the given figure, AOB is a straight line. If ∠AOC + ∠BOD = 85°, then ∠COD =
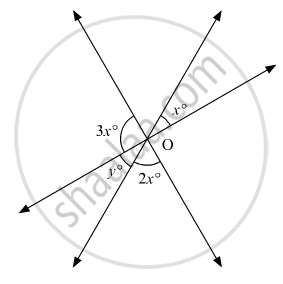
In the given figure, the value of y is
Give two examples of parallel lines you can see in your environment.
Give two examples of perpendicular lines you can see in your environment.
Look at the picture given below. Decide whether the lines given in picture is parallel or perpendicular to each other and write the answer in the box.

Mention two real life situations where we use parallel lines
