Advertisements
Advertisements
प्रश्न
If the median to the base of a triangle is perpendicular to the base, then triangle is isosceles.
उत्तर
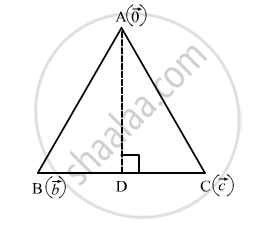
Let ∆ABC be a triangle such that AD is the median. Taking A as the origin, let the position vectors of B and C be \[\vec{b}\] and \[\vec{c}\] respectively.
Then,
Position vector of D = \[\frac{\vec{b} + \vec{c}}{2}\].....................(Mid-point formula)
Now,
\[\vec{AD}\] = Position vector of D − Position vector of A =\[\frac{\vec{b} + \vec{c}}{2}\]
\[\vec{BC}\] = Position vector of C − Position vector of B= \[\vec{c} - \vec{b}\]
Since
\[\vec{AD} \perp \vec{BC}\]
\[\therefore \vec{AD} . \vec{BC} = 0\]
\[ \Rightarrow \frac{1}{2}\left( \vec{b} + \vec{c} \right) . \left( \vec{c} - \vec{b} \right) = 0\]
\[ \Rightarrow \left( \vec{c} + \vec{b} \right) . \left( \vec{c} - \vec{b} \right) = 0\]
\[ \Rightarrow \left| \vec{c} \right|^2 - \left| \vec{b} \right|^2 = 0\]
\[ \Rightarrow \left| \vec{c} \right| = \left| \vec{b} \right|\]
\[ \Rightarrow AC = AB \]
Hence, the ∆ABC is an isosceles triangle.
APPEARS IN
संबंधित प्रश्न
If `bar p = hat i - 2 hat j + hat k and bar q = hat i + 4 hat j - 2 hat k` are position vector (P.V.) of points P and Q, find the position vector of the point R which divides segment PQ internally in the ratio 2:1
By vector method prove that the medians of a triangle are concurrent.
Show that the points A (1, –2, –8), B (5, 0, –2) and C (11, 3, 7) are collinear, and find the ratio in which B divides AC.
If the origin is the centroid of the triangle whose vertices are A(2, p, –3), B(q, –2, 5) and C(–5, 1, r), then find the values of p, q, r.
Prove by vector method that the sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of its sides.
If AD is the median of ∆ABC, using vectors, prove that \[{AB}^2 + {AC}^2 = 2\left( {AD}^2 + {CD}^2 \right)\]
In a quadrilateral ABCD, prove that \[{AB}^2 + {BC}^2 + {CD}^2 + {DA}^2 = {AC}^2 + {BD}^2 + 4 {PQ}^2\] where P and Q are middle points of diagonals AC and BD.
Let `A (bara)` and `B (barb)` are any two points in the space and `"R"(bar"r")` be a point on the line segment AB dividing it internally in the ratio m : n, then prove that `bar r = (mbarb + nbara)/(m + n) `
Find the position vector of point R which divides the line joining the points P and Q whose position vectors are `2hat"i" - hat"j" + 3hat"k"` and `- 5hat"i" + 2hat"j" - 5hat"k"` in the ratio 3 : 2 is externally.
Find the position vector of midpoint M joining the points L(7, –6, 12) and N(5, 4, –2).
If the points A(3, 0, p), B(–1, q, 3) and C(–3, 3, 0) are collinear, then find
- the ratio in which the point C divides the line segment AB
- the values of p and q.
In Δ OAB, E is the midpoint of OB and D is the point on AB such that AD : DB = 2 : 1. If OD and AE intersect at P, then determine the ratio OP : PD using vector methods.
Find the centroid of tetrahedron with vertices K(5, −7, 0), L(1, 5, 3), M(4, −6, 3), N(6, −4, 2)
The points A, B, C have position vectors `bar"a", bar"b" and bar"c"` respectively. The point P is the midpoint of AB. Find the vector `bar"PC"` in terms of `bar"a", bar"b", bar"c"`.
Find the volume of a parallelopiped whose coterimus edges are represented by the vectors `hat"i" + hat"k", hat"i" + hat"k", hat"i" + hat"j"`. Also find volume of tetrahedron having these coterminus edges.
Find the position vector of point R which divides the line joining the points P and Q whose position vectors are `2hat"i" - hat"j" + 3hat"k"` and `-5hat"i" + 2hat"j" - 5hat"k"` in the ratio 3:2
(i) internally
(ii) externally
Using vector method, find the incenter of the triangle whose vertices are A(0, 3, 0), B(0, 0, 4) and C(0, 3, 4)
If the plane 2x + 3y + 5z = 1 intersects the co-ordinate axes at the points A, B, C, then the centroid of Δ ABC is ______.
In a triangle ABC, if `1/(a + c) + 1/(b + c) = 3/(a + b + c)` then angle C is equal to ______
If G and G' are the centroids of the triangles ABC and A'B'C', then `overline("A""A"^') + overline("B""B"^') + overline("C""C"^')` is equal to ______
The image of the point (1, 6, 3) in the line `x/1 = (y - 1)/2 = (z - 2)/3` is ______
If the orthocentre and circumcentre of a triangle are (-3, 5, 1) and (6, 2, -2) respectively, then its centroid is ______
The co-ordinates of the points which divides line segment joining the point A(2, –6, 8) and B(–1, 3,–4) internally in the ratio 1: 3' are ______.
Let `square`PQRS be a quadrilateral. If M and N are midpoints of the sides PQ and RS respectively then `bar"PS" + bar"OR"` = ______.
In ΔABC the mid-point of the sides AB, BC and CA are respectively (l, 0, 0), (0, m, 0) and (0, 0, n). Then, `("AB"^2 + "BC"^2 + "CA"^2)/("l"^2 + "m"^2 + "n"^2)` is equal to ______.
If `overlinea, overlineb, overlinec` are the position vectors of the points A, B, C respectively and `5overlinea + 3overlineb - 8overlinec = overline0` then find the ratio in which the point C divides the line segment AB.
The position vectors of three consecutive vertices of a parallelogram ABCD are `A(4hati + 2hatj - 6hatk), B(5hati - 3hatj + hatk)`, and `C(12hati + 4hatj + 5hatk)`. The position vector of D is given by ______.
Using vector method, prove that the perpendicular bisectors of sides of a triangle are concurrent.
If `bara, barb, barc` are the position vectors of the points A, B, C respectively and `5 bar a - 3 bar b - 2 bar c = bar 0`, then find the ratio in which the point C divides the line segment BA.
The position vector of points A and B are `6bara + 2 barb and bara - 3 barb`. If point C divides AB in the ratio 3 : 2, then show that the position vector of C is `3bara - barb`.
The position vector of points A and B are `6 bara + 2barb and bara - 3barb.` If the point C divides AB in the ratio 3 : 2 then show that the position vector of C is `3bara - barb.`
The position vector of points A and B are 6`bara + 2barb and bara - 3barb`. If the point C divides AB in the ratio 3 : 2 then show that the position vector of C is 3`bara - barb`.
The position vectors of points A and B are 6`bara` + 2`barb` and `bara - 3barb`. If the point C divides AB in the ratio 3:2, then show that the position vector of C is 3`bara - b`.
