Advertisements
Advertisements
प्रश्न
By vector method prove that the medians of a triangle are concurrent.
Using vector method prove that the medians of a triangle are concurrent.
उत्तर
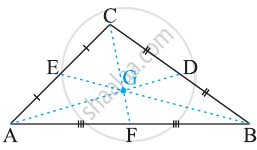
Let A, B and C be vertices of a triangle.
Let D, E and F be the mid-points of the sides BC, AC and AB respectively.
Let `bara, barb, barc, bard, bare` and `barf` be position vectors of points A, B, C, D, E and F respectively.
Therefore, by mid-point formula,
∴ `bard = (barb + barc)/2, bare = (bara + barc)/2` and `barf = (bara + barb)/2`
∴ `2bard = barb + barc, 2bare = bara + barc` and `2barf = bara + barb`
∴ `2bard + bara = bara + barb + barc`, similarly `2bare + barb = 2barf + barc = bara + barb + barc`
∴ `(2bard + bara)/3 = (2bare + barb)/3 = (2barf + barc)/3 = (bara + barb + barc)/3 = barg` ...(Say)
Then we have `barg = (bara + barb + barc)/3 = ((2)bard + (1)bara)/(2 + 1) = ((2)bare + (1)barb)/(2 + 1) = ((2)barf + (1)barc)/(2 + 1)`
If G is the point whose position vector is `barg`, then from the above equation it is clear that the point G lies on the medians AD, BE, CF and it divides each of the medians AD, BE, CF internally in the ratio 2 : 1.
Therefore, three medians are concurrent.
APPEARS IN
संबंधित प्रश्न
If `bar p = hat i - 2 hat j + hat k and bar q = hat i + 4 hat j - 2 hat k` are position vector (P.V.) of points P and Q, find the position vector of the point R which divides segment PQ internally in the ratio 2:1
Show that the points A (1, –2, –8), B (5, 0, –2) and C (11, 3, 7) are collinear, and find the ratio in which B divides AC.
If the origin is the centroid of the triangle whose vertices are A(2, p, –3), B(q, –2, 5) and C(–5, 1, r), then find the values of p, q, r.
In a triangle OAB,\[\angle\]AOB = 90º. If P and Q are points of trisection of AB, prove that \[{OP}^2 + {OQ}^2 = \frac{5}{9} {AB}^2\]
Prove by vector method that the sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of its sides.
Prove using vectors: The quadrilateral obtained by joining mid-points of adjacent sides of a rectangle is a rhombus.
If the median to the base of a triangle is perpendicular to the base, then triangle is isosceles.
Find the position vector of point R which divides the line joining the points P and Q whose position vectors are `2hati - hatj + 3hatk` and `- 5hati + 2hatj - 5hatk` in the ratio 3:2 is internally.
Find the position vector of midpoint M joining the points L(7, –6, 12) and N(5, 4, –2).
The position vector of points A and B are `6bar"a" + 2bar"b"` and `bar"a" - 3bar"b"`. If the point C divides AB in the ratio 3 : 2, show that the position vector of C is `3bar"a" - bar"b"`.
Prove that the line segments joining the midpoints of the adjacent sides of a quadrilateral form a parallelogram.
Prove that the median of a trapezium is parallel to the parallel sides of the trapezium and its length is half of the sum of the lengths of the parallel sides.
If two of the vertices of a triangle are A (3, 1, 4) and B(− 4, 5, −3) and the centroid of the triangle is at G (−1, 2, 1), then find the coordinates of the third vertex C of the triangle.
Find the centroid of tetrahedron with vertices K(5, −7, 0), L(1, 5, 3), M(4, −6, 3), N(6, −4, 2)
The points A, B, C have position vectors `bar"a", bar"b" and bar"c"` respectively. The point P is the midpoint of AB. Find the vector `bar"PC"` in terms of `bar"a", bar"b", bar"c"`.
If D, E, F are the midpoints of the sides BC, CA, AB of a triangle ABC, prove that `bar"AD" + bar"BE" + bar"CF" = bar0`.
Prove that `(bar"a" xx bar"b").(bar"c" xx bar"d")` =
`|bar"a".bar"c" bar"b".bar"c"|`
`|bar"a".bar"d" bar"b".bar"d"|.`
Find the volume of a parallelopiped whose coterimus edges are represented by the vectors `hat"i" + hat"k", hat"i" + hat"k", hat"i" + hat"j"`. Also find volume of tetrahedron having these coterminus edges.
Find the position vector of point R which divides the line joining the points P and Q whose position vectors are `2hat"i" - hat"j" + 3hat"k"` and `-5hat"i" + 2hat"j" - 5hat"k"` in the ratio 3:2
(i) internally
(ii) externally
If A(5, 1, p), B(1, q, p) and C(1, −2, 3) are vertices of triangle and `"G"("r", -4/3, 1/3)` is its centroid then find the values of p, q and r
Prove that the angle bisectors of a triangle are concurrent
Using vector method, find the incenter of the triangle whose vertices are A(0, 3, 0), B(0, 0, 4) and C(0, 3, 4)
If the plane 2x + 3y + 5z = 1 intersects the co-ordinate axes at the points A, B, C, then the centroid of Δ ABC is ______.
Let G be the centroid of a Δ ABC and O be any other point in that plane, then OA + OB + OC + CG = ?
In a triangle ABC, if `1/(a + c) + 1/(b + c) = 3/(a + b + c)` then angle C is equal to ______
If G(3, -5, r) is centroid of triangle ABC where A(7, - 8, 1), B(p, q, 5) and C(q + 1, 5p, 0) are vertices of a triangle then values of p, q, rare respectively.
If P(2, 2), Q(- 2, 4) and R(3, 4) are the vertices of Δ PQR then the equation of the median through vertex R is ______.
If the position vectors of points A and B are `hati + 8hatj + 4hatk` and `7hati + 2hatj - 8hatk`, then what will be the position vector of the midpoint of AB?
If G and G' are the centroids of the triangles ABC and A'B'C', then `overline("A""A"^') + overline("B""B"^') + overline("C""C"^')` is equal to ______
The image of the point (1, 6, 3) in the line `x/1 = (y - 1)/2 = (z - 2)/3` is ______
If M and N are the midpoints of the sides BC and CD respectively of a parallelogram ABCD, then `overline(AM) + overline(AN)` = ______
If G`(overlineg)` is the centroid, `H(overlineh)` is the orthocentre and P`(overlinep)` is the circumcentre of a triangle and `xoverlinep + yoverlineh + zoverlineg = 0`, then ______
If `3bar"a" + 5bar"b" = 8bar"c"`, then A divides BC in tbe ratio ______.
Let `square`PQRS be a quadrilateral. If M and N are midpoints of the sides PQ and RS respectively then `bar"PS" + bar"OR"` = ______.
In ΔABC, P is the midpoint of BC, Q divides CA internally in the ratio 2:1 and R divides AB externally in the ratio 1:2, then ______.
Find the unit vector in the diret:tion of the vector `veca = hati + hatj + 2hatk`
M and N are the mid-points of the diagonals AC and BD respectively of quadrilateral ABCD, then AB + AD + CB + CD is equal to ______.
The position vector of points A and B are `6 bar "a" + 2 bar "b" and bar "a" - 3 bar"b"`. If the point C divided AB in the ratio 3 : 2, show that the position vector of C is `3 bar "a" - bar "b".`
The position vector of points A and B are `6bara +2barb ` and `bara-3barb `.If the point C divides AB in the ratio 3 : 2 then show that the position vector of C is `3bara-barb` .
If `bara, barb` and `barr` are position vectors of the points A, B and R respectively and R divides the line segment AB externally in the ratio m : n, then prove that `barr = (mbarb - nbara)/(m - n)`.
Using vector method, prove that the perpendicular bisectors of sides of a triangle are concurrent.
Let `A(bara)` and `B(barb)` be any two points in the space and `R(barr)` be the third point on the line AB dividing the segment AB externally in the ratio m : n, then prove that `barr = (mbarb - nbara)/(m - n)`.
AB and CD are two chords of a circle intersecting at right angles to each other at P. If R is the centre of the circle, prove that:
`bar(PA) + bar(PB) + bar(PC) + bar(PD) = 2bar(PR)`
The position vector of points A and B are `6bara + 2 barb and bara - 3 barb`. If point C divides AB in the ratio 3 : 2, then show that the position vector of C is `3bara - barb`.
The position vector of points A and B are `6bara + 2 barb and bara - 3 barb`. If point C divides AB in the ratio 3 : 2, then show that the position vector of C is `3bara - barb`.
The position vector of points A and B are `6bara + 2 barb` and `bara-3 barb`. If the point C divides AB in the ratio 3 : 2 then show that the position vector of C is `3bara -barb`.
The position vector of points A and B are `6 bara + 2 barb and bara - 3 barb`. If the point C divides AB in the ratio 3 : 2 then show that the position vector of C is `3 bara - barb`.
The position vector of points A and B are 6`bara + 2barb and bara - 3barb`. If the point C divides AB in the ratio 3 : 2 then show that the position vector of C is 3`bara - barb`.
