Advertisements
Advertisements
प्रश्न
Prove using vectors: The quadrilateral obtained by joining mid-points of adjacent sides of a rectangle is a rhombus.
उत्तर
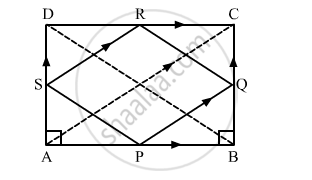
ABCD is a rectangle. Let P, Q, R and S be the mid-points of the sides AB, BC, CD and DA, respectively.
Now,
\[\vec{PQ} = \vec{PB} + \vec{BQ} = \frac{1}{2} \vec{AB} + \frac{1}{2} \vec{BC} = \frac{1}{2}\left( \vec{AB} + \vec{BC} \right) = \frac{1}{2} \vec{AC}\]..............( 1 )
\[\vec{SR} = \vec{SD} + \vec{DR} = \frac{1}{2} \vec{AD} + \frac{1}{2} \vec{DC} = \frac{1}{2}\left( \vec{AD} + \vec{DC} \right) = \frac{1}{2} \vec{AC}\] ...............( 2 )
From (1) and (2), we have
\[\vec{PQ} = \vec{SR}\]
So, the sides PQ and SR are equal and parallel. Thus, PQRS is a parallelogram.
Now,
\[\left| \vec{PQ} \right|^2 = \vec{PQ} . \vec{PQ} \]
\[ \Rightarrow \left| \vec{PQ} \right|^2 = \left( \vec{PB} + \vec{BQ} \right) . \left( \vec{PB} + \vec{BQ} \right)\]
\[ \Rightarrow \left| \vec{PQ} \right|^2 = \left| \vec{PB} \right|^2 + 2 \vec{PB} . \vec{BQ} + \left| \vec{BQ} \right|^2 \]
\[ \Rightarrow \left| \vec{PQ} \right|^2 = \left| \vec{PB} \right|^2 + 0 + \left| \vec{BQ} \right|^2 \left( \vec{PB} \perp \vec{BQ} \right)\]
\[ \Rightarrow \left| \vec{PQ} \right|^2 = \left| \vec{PB} \right|^2 + \left| \vec{BQ} \right|^2 ....................\left( 3 \right)\]
Also,
\[\left| \vec{PS} \right|^2 = \vec{PS} . \vec{PS} \]
\[ \Rightarrow \left| \vec{PS} \right|^2 = \left( \vec{PA} + \vec{AS} \right) . \left( \vec{PA} + \vec{AS} \right)\]
\[ \Rightarrow \left| \vec{PS} \right|^2 = \left| \vec{PA} \right|^2 + 2 \vec{PA} . \vec{AS} + \left| \vec{AS} \right|^2 \]
\[ \Rightarrow \left| \vec{PS} \right|^2 = \left| \vec{PB} \right|^2 + 0 + \left| \vec{BQ} \right|^2 \left( \vec{PA} \perp \vec{AS} \right)\]
\[ \Rightarrow \left| \vec{PS} \right|^2 = \left| \vec{PB} \right|^2 + \left| \vec{BQ} \right|^2........................\left( 4 \right)\]
From (3) and (4), we have
\[\left| \vec{PQ} \right|^2 = \left| \vec{PS} \right|^2 \]
\[ \Rightarrow \left| \vec{PQ} \right| = \left| \vec{PS} \right|\]
So, the adjacent sides of the parallelogram are equal. Hence, PQRS is a rhombus.
APPEARS IN
संबंधित प्रश्न
By vector method prove that the medians of a triangle are concurrent.
If point C `(barc)` divides the segment joining the points A(`bara`) and B(`barb`) internally in the ratio m : n, then prove that `barc=(mbarb+nbara)/(m+n)`
Find the coordinate of the point P where the line through A(3, –4, –5) and B(2, –3, 1) crosses the plane passing through three points L(2, 2, 1), M(3, 0, 1) and N(4, –1, 0).
Also, find the ratio in which P divides the line segment AB.
Show that the points A (1, –2, –8), B (5, 0, –2) and C (11, 3, 7) are collinear, and find the ratio in which B divides AC.
If the origin is the centroid of the triangle whose vertices are A(2, p, –3), B(q, –2, 5) and C(–5, 1, r), then find the values of p, q, r.
Prove that the diagonals of a rhombus are perpendicular bisectors of each other.
Let `A (bara)` and `B (barb)` are any two points in the space and `"R"(bar"r")` be a point on the line segment AB dividing it internally in the ratio m : n, then prove that `bar r = (mbarb + nbara)/(m + n) `
Find the position vector of midpoint M joining the points L(7, –6, 12) and N(5, 4, –2).
Prove that a quadrilateral is a parallelogram if and only if its diagonals bisect each other.
In Δ OAB, E is the midpoint of OB and D is the point on AB such that AD : DB = 2 : 1. If OD and AE intersect at P, then determine the ratio OP : PD using vector methods.
If the centroid of a tetrahedron OABC is (1, 2, - 1) where A(a, 2, 3), B(1, b, 2), C(2, 1, c), find the distance of P(a, b, c) from origin.
If D, E, F are the midpoints of the sides BC, CA, AB of a triangle ABC, prove that `bar"AD" + bar"BE" + bar"CF" = bar0`.
Find the volume of a parallelopiped whose coterimus edges are represented by the vectors `hat"i" + hat"k", hat"i" + hat"k", hat"i" + hat"j"`. Also find volume of tetrahedron having these coterminus edges.
Find the position vector of point R which divides the line joining the points P and Q whose position vectors are `2hat"i" - hat"j" + 3hat"k"` and `-5hat"i" + 2hat"j" - 5hat"k"` in the ratio 3:2
(i) internally
(ii) externally
If A(5, 1, p), B(1, q, p) and C(1, −2, 3) are vertices of triangle and `"G"("r", -4/3, 1/3)` is its centroid then find the values of p, q and r
Prove that altitudes of a triangle are concurrent
Let G be the centroid of a Δ ABC and O be any other point in that plane, then OA + OB + OC + CG = ?
In a quadrilateral ABCD, M and N are the mid-points of the sides AB and CD respectively. If AD + BC = tMN, then t = ____________.
In a triangle ABC, if `1/(a + c) + 1/(b + c) = 3/(a + b + c)` then angle C is equal to ______
If G(3, -5, r) is centroid of triangle ABC where A(7, - 8, 1), B(p, q, 5) and C(q + 1, 5p, 0) are vertices of a triangle then values of p, q, rare respectively.
If P(2, 2), Q(- 2, 4) and R(3, 4) are the vertices of Δ PQR then the equation of the median through vertex R is ______.
The image of the point (1, 6, 3) in the line `x/1 = (y - 1)/2 = (z - 2)/3` is ______
If M and N are the midpoints of the sides BC and CD respectively of a parallelogram ABCD, then `overline(AM) + overline(AN)` = ______
If G`(overlineg)` is the centroid, `H(overlineh)` is the orthocentre and P`(overlinep)` is the circumcentre of a triangle and `xoverlinep + yoverlineh + zoverlineg = 0`, then ______
The co-ordinates of the points which divides line segment joining the point A(2, –6, 8) and B(–1, 3,–4) internally in the ratio 1: 3' are ______.
In ΔABC, P is the midpoint of BC, Q divides CA internally in the ratio 2:1 and R divides AB externally in the ratio 1:2, then ______.
If D, E, F are the mid points of the sides BC, CA and AB respectively of a triangle ABC and 'O' is any point, then, `|vec(AD) + vec(BE) + vec(CF)|`, is ______.
In ΔABC the mid-point of the sides AB, BC and CA are respectively (l, 0, 0), (0, m, 0) and (0, 0, n). Then, `("AB"^2 + "BC"^2 + "CA"^2)/("l"^2 + "m"^2 + "n"^2)` is equal to ______.
If G(g), H(h) and (p) are centroid orthocentre and circumcentre of a triangle and xp + yh + zg = 0, then (x, y, z) is equal to ______.
AB and CD are two chords of a circle intersecting at right angles to each other at P. If R is the centre of the circle, prove that:
`bar(PA) + bar(PB) + bar(PC) + bar(PD) = 2bar(PR)`
The position vector of points A and B are `6bara + 2 barb` and `bara-3 barb`. If the point C divides AB in the ratio 3 : 2 then show that the position vector of C is `3bara -barb`.
The position vector of points A and B are `6bara + 2barb` and `bara - 3barb`. If the point C divides AB in the ratio 3 : 2, then show that the position vector of C is `3bara - barb`.
The position vector of points A and B are `6 bara + 2barb and bara - 3barb.` If the point C divides AB in the ratio 3 : 2 then show that the position vector of C is `3bara - barb.`
The position vectors of points A and B are 6`bara` + 2`barb` and `bara - 3barb`. If the point C divides AB in the ratio 3:2, then show that the position vector of C is 3`bara - b`.
