Advertisements
Advertisements
प्रश्न
Prove using vectors: The quadrilateral obtained by joining mid-points of adjacent sides of a rectangle is a rhombus.
उत्तर
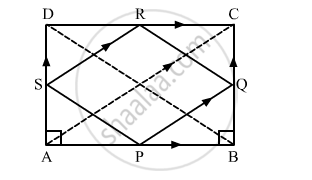
ABCD is a rectangle. Let P, Q, R and S be the mid-points of the sides AB, BC, CD and DA, respectively.
Now,
\[\vec{PQ} = \vec{PB} + \vec{BQ} = \frac{1}{2} \vec{AB} + \frac{1}{2} \vec{BC} = \frac{1}{2}\left( \vec{AB} + \vec{BC} \right) = \frac{1}{2} \vec{AC}\]..............( 1 )
\[\vec{SR} = \vec{SD} + \vec{DR} = \frac{1}{2} \vec{AD} + \frac{1}{2} \vec{DC} = \frac{1}{2}\left( \vec{AD} + \vec{DC} \right) = \frac{1}{2} \vec{AC}\] ...............( 2 )
From (1) and (2), we have
\[\vec{PQ} = \vec{SR}\]
So, the sides PQ and SR are equal and parallel. Thus, PQRS is a parallelogram.
Now,
\[\left| \vec{PQ} \right|^2 = \vec{PQ} . \vec{PQ} \]
\[ \Rightarrow \left| \vec{PQ} \right|^2 = \left( \vec{PB} + \vec{BQ} \right) . \left( \vec{PB} + \vec{BQ} \right)\]
\[ \Rightarrow \left| \vec{PQ} \right|^2 = \left| \vec{PB} \right|^2 + 2 \vec{PB} . \vec{BQ} + \left| \vec{BQ} \right|^2 \]
\[ \Rightarrow \left| \vec{PQ} \right|^2 = \left| \vec{PB} \right|^2 + 0 + \left| \vec{BQ} \right|^2 \left( \vec{PB} \perp \vec{BQ} \right)\]
\[ \Rightarrow \left| \vec{PQ} \right|^2 = \left| \vec{PB} \right|^2 + \left| \vec{BQ} \right|^2 ....................\left( 3 \right)\]
Also,
\[\left| \vec{PS} \right|^2 = \vec{PS} . \vec{PS} \]
\[ \Rightarrow \left| \vec{PS} \right|^2 = \left( \vec{PA} + \vec{AS} \right) . \left( \vec{PA} + \vec{AS} \right)\]
\[ \Rightarrow \left| \vec{PS} \right|^2 = \left| \vec{PA} \right|^2 + 2 \vec{PA} . \vec{AS} + \left| \vec{AS} \right|^2 \]
\[ \Rightarrow \left| \vec{PS} \right|^2 = \left| \vec{PB} \right|^2 + 0 + \left| \vec{BQ} \right|^2 \left( \vec{PA} \perp \vec{AS} \right)\]
\[ \Rightarrow \left| \vec{PS} \right|^2 = \left| \vec{PB} \right|^2 + \left| \vec{BQ} \right|^2........................\left( 4 \right)\]
From (3) and (4), we have
\[\left| \vec{PQ} \right|^2 = \left| \vec{PS} \right|^2 \]
\[ \Rightarrow \left| \vec{PQ} \right| = \left| \vec{PS} \right|\]
So, the adjacent sides of the parallelogram are equal. Hence, PQRS is a rhombus.
APPEARS IN
संबंधित प्रश्न
Find the coordinate of the point P where the line through A(3, –4, –5) and B(2, –3, 1) crosses the plane passing through three points L(2, 2, 1), M(3, 0, 1) and N(4, –1, 0).
Also, find the ratio in which P divides the line segment AB.
Prove that the diagonals of a rectangle are perpendicular if and only if the rectangle is a square.
If the median to the base of a triangle is perpendicular to the base, then triangle is isosceles.
Let `A (bara)` and `B (barb)` are any two points in the space and `"R"(bar"r")` be a point on the line segment AB dividing it internally in the ratio m : n, then prove that `bar r = (mbarb + nbara)/(m + n) `
Find the position vector of point R which divides the line joining the points P and Q whose position vectors are `2hati - hatj + 3hatk` and `- 5hati + 2hatj - 5hatk` in the ratio 3:2 is internally.
Prove that the line segments joining the midpoints of the adjacent sides of a quadrilateral form a parallelogram.
Prove that a quadrilateral is a parallelogram if and only if its diagonals bisect each other.
In Δ OAB, E is the midpoint of OB and D is the point on AB such that AD : DB = 2 : 1. If OD and AE intersect at P, then determine the ratio OP : PD using vector methods.
The points A, B, C have position vectors `bar"a", bar"b" and bar"c"` respectively. The point P is the midpoint of AB. Find the vector `bar"PC"` in terms of `bar"a", bar"b", bar"c"`.
If D, E, F are the midpoints of the sides BC, CA, AB of a triangle ABC, prove that `bar"AD" + bar"BE" + bar"CF" = bar0`.
If `bara, barb` and `barc` are position vectors of the points A, B, C respectively and `5bara - 3barb - 2barc = bar0`, then find the ratio in which the point C divides the line segement BA.
If G(a, 2, −1) is the centroid of the triangle with vertices P(1, 2, 3), Q(3, b, −4) and R(5, 1, c) then find the values of a, b and c
If A(5, 1, p), B(1, q, p) and C(1, −2, 3) are vertices of triangle and `"G"("r", -4/3, 1/3)` is its centroid then find the values of p, q and r
Prove that altitudes of a triangle are concurrent
Prove that the angle bisectors of a triangle are concurrent
Using vector method, find the incenter of the triangle whose vertices are A(0, 3, 0), B(0, 0, 4) and C(0, 3, 4)
In a quadrilateral ABCD, M and N are the mid-points of the sides AB and CD respectively. If AD + BC = tMN, then t = ____________.
P is the point of intersection of the diagonals of the parallelogram ABCD. If O is any point, then `overline"OA" + overline"OB" + overline"OC" + overline"OD"` = ______
If the position vectors of points A and B are `hati + 8hatj + 4hatk` and `7hati + 2hatj - 8hatk`, then what will be the position vector of the midpoint of AB?
The image of the point (1, 6, 3) in the line `x/1 = (y - 1)/2 = (z - 2)/3` is ______
If `3bar"a" + 5bar"b" = 8bar"c"`, then A divides BC in tbe ratio ______.
If A, B, C are the vertices of a triangle whose position vectors are `overline("a"),overline("b"),overline("c")` and G is the centroid of the `triangle ABC,` then `overline("GA")+overline("GB")+overline("GC")` is ______.
Find the unit vector in the diret:tion of the vector `veca = hati + hatj + 2hatk`
If D, E, F are the mid points of the sides BC, CA and AB respectively of a triangle ABC and 'O' is any point, then, `|vec(AD) + vec(BE) + vec(CF)|`, is ______.
The position vector of points A and B are `6 bar "a" + 2 bar "b" and bar "a" - 3 bar"b"`. If the point C divided AB in the ratio 3 : 2, show that the position vector of C is `3 bar "a" - bar "b".`
The position vector of points A and B are `6bara +2barb ` and `bara-3barb `.If the point C divides AB in the ratio 3 : 2 then show that the position vector of C is `3bara-barb` .
If `bara, barb` and `barr` are position vectors of the points A, B and R respectively and R divides the line segment AB externally in the ratio m : n, then prove that `barr = (mbarb - nbara)/(m - n)`.
If `bara, barb, barc` are the position vectors of the points A, B, C respectively and `5 bar a - 3 bar b - 2 bar c = bar 0`, then find the ratio in which the point C divides the line segment BA.
The position vector of points A and B are `6bara + 2 barb and bara - 3 barb`. If point C divides AB in the ratio 3 : 2, then show that the position vector of C is `3bara - barb`.
The position vector of points A and B are `6 bara + 2barb and bara - 3barb.` If the point C divides AB in the ratio 3 : 2 then show that the position vector of C is `3bara - barb.`
The position vector of points A and B are `6 bara + 2 barb and bara - 3 barb`. If the point C divides AB in the ratio 3 : 2 then show that the position vector of C is `3 bara - barb`.
The position vector of points A and B are 6`bara + 2barb and bara - 3barb`. If the point C divides AB in the ratio 3 : 2 then show that the position vector of C is 3`bara - barb`.
The position vectors of points A and B are 6`bara` + 2`barb` and `bara - 3barb`. If the point C divides AB in the ratio 3:2, then show that the position vector of C is 3`bara - b`.
