Advertisements
Advertisements
प्रश्न
If the first term of an A.P. is p, second term is q and last term is r, then show that sum of all terms is `(q + r - 2p) xx ((p + r))/(2(q - p))`.
Advertisements
उत्तर
Given: First term (t1) = a = p, Second term (t2) = q, tn = r
Common difference (d) = t2 – t1 = q – p
According to the question,
tn = a + (n – 1) × d
r = p + (n – 1) × (q – p)
(r – p) = (n – 1) × (q – p)
n – 1 = `(r - p)/(q - p)`
n = `(r - p)/(q - p) + 1`
n = `(r - p + q - p)/(q - p)`
n = `(r + q - 2p)/(q - p)`
We know
Sn = `n/2[2a + (n - 1)d]`
= `(r + q - 2p)/(2(q - p)) [2p + ((r + q - 2p)/(q - p) - 1) (q - p)]`
= `(r + q - 2p)/(2(q - p)) [2p + ((r + q - 2p - (q - p))/(q - p)) (q - p)]`
= `(r + q - 2p)/(2(q - p)) [((r + q - 2p - q + p)/(q - p)) (q - p)]`
= `(r + q - 2p)/(2(q - p))[2p + ((r - p)/(q - p)) (q - p)]`
= `(r + q - 2p)/(2(q - p))[2p + r - p]`
= `(r + q - 2p)/(2(q - p))[r + p]`
Sn = `(q + r - 2p) xx ((p + r))/(2(q - p))`
Hence proved.
APPEARS IN
संबंधित प्रश्न
Find the sum given below:
34 + 32 + 30 + ... + 10
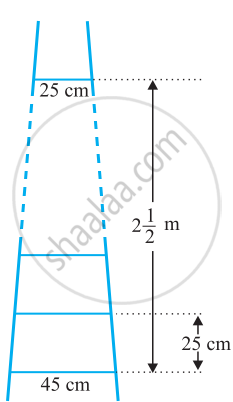
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
Show that the sum of all odd integers between 1 and 1000 which are divisible by 3 is 83667.
Find the sum of all integers between 100 and 550, which are divisible by 9.
In an A.P., if the 5th and 12th terms are 30 and 65 respectively, what is the sum of first 20 terms?
If numbers n – 2, 4n – 1 and 5n + 2 are in A.P., find the value of n and its next two terms.
The fourth term of an A.P. is 11 and the eighth term exceeds twice the fourth term by 5. Find the A.P. and the sum of first 50 terms.
If the numbers a, 9, b, 25 from an AP, find a and b.
Write the next term for the AP` sqrt( 8), sqrt(18), sqrt(32),.........`
If the sum of first n terms is (3n2 + 5n), find its common difference.
Find the first term and common difference for the A.P.
`1/4,3/4,5/4,7/4,...`
Choose the correct alternative answer for the following question.
For an given A.P. a = 3.5, d = 0, n = 101, then tn = ....
In an A.P. the first term is – 5 and the last term is 45. If the sum of all numbers in the A.P. is 120, then how many terms are there? What is the common difference?
Write the value of x for which 2x, x + 10 and 3x + 2 are in A.P.
If `4/5` , a, 2 are three consecutive terms of an A.P., then find the value of a.
Q.17
If the sum of the first four terms of an AP is 40 and that of the first 14 terms is 280. Find the sum of its first n terms.
Find the sum of all the 11 terms of an A.P. whose middle most term is 30.
Find the sum of first seven numbers which are multiples of 2 as well as of 9.
If the first term of an A.P. is 5, the last term is 15 and the sum of first n terms is 30, then find the value of n.
