Advertisements
Advertisements
प्रश्न
If two straight lines intersect each other, prove that the ray opposite to the bisector of one of the angles thus formed bisects the vertically opposite angle.
उत्तर
Let AB and CD intersect at a point O
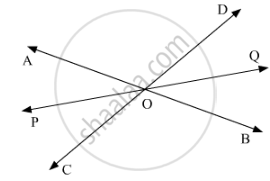
Also, let us draw the bisector OP of ∠AOC.
Therefore,
∠AOP = ∠POC (1)
Also, let’s extend OP to Q.
We need to show that, OQ bisects ∠BOD.
Let us assume that OQ bisects∠BOD, now we shall prove that POQ is a line.
We know that,
∠AOCand ∠DOBare vertically opposite angles. Therefore, these must be equal, that is:
∠AOC = ∠DOB (2)
∠AOPand ∠BOQ are vertically opposite angles. Therefore,
∠AOP = ∠BOQ
Similarly,
∠POC = ∠DOQ
We know that:
∠AOP +∠AOD+∠DOQ+∠POC+∠BOC+∠BOQ = 360°
2∠AOP+∠AOD+2∠DOQ+∠BOC =360°
2∠AOP + 2∠AOD+ 2∠DOQ = 360°
2(∠AOP+∠AOD+ ∠DOQ) = 360°
∠AOP+∠AOD+ ∠DOQ = `(360°)/2`
∠AOP+∠AOD+ ∠DOQ = 180°
Thus, POQ is a straight line.
Hence our assumption is correct. That is,
We can say that if the two straight lines intersect each other, then the ray opposite to the bisector of one of the angles thus formed bisects the vertically opposite angles.
APPEARS IN
संबंधित प्रश्न
Fill in the blank so as to make the following statement true:
A ray stands on a line, then the sum of the two adjacent angles so formed is ______
Two straight lines AB and CD cut each other at O. If ∠BOD = 63°, then ∠BOC =
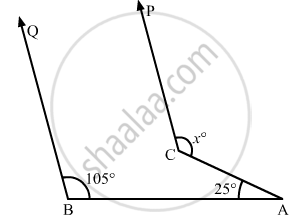
In the given figure, if CP || DQ, then the measure of x is
State, true or false:
An infinite number of straight lines can be drawn through a given point.
State, true or false:
Is 45° the supplement of 45°?
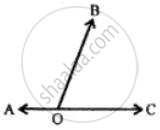
In the following figure, ∠AOB and ∠AOC are adjacent angles? Give the reason for your answer.
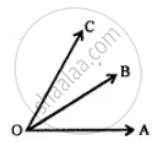
In the following figure, ∠AOB and ∠AOC are adjacent angles? Give the reason for your answer.
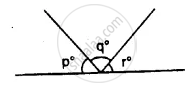
In the given figure. p° = q° = r°, find each.
Write the complement of (x + 5)°
Write the supplement of (x + 35)°
